18.2.4. Среднее квадратическое отклонение

Одной из основных оценок рассеяния возможных значе­ний случайной величины служит Среднее квадратическое от­клонение.

Определение 4. Средним квадратическим отклонением слу­чайной величины Х (стандартом) называется квадратный ко­рень из ее дисперсии:

Согласно этому определению, из свойства 3 и формулы (18.13) следует, что в случае суммы взаимно независимых слу­чайных величин справедлива формула

Пример 9. Найти дисперсию и среднее квадратическое отклонение случайной величины X, заданной следующим распределением:

Решение. Имеем М(Х) = 2,6. Составим таблицу распре­деления случайной величины X2:

Отсюда получаем, что М(Х2) = 14,4. По формулам (18.11) и (18.15) окончательно получаем искомые значения D(X) И. σ(Х):

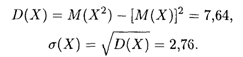
Пример 10. Законы распределения независимых случайных величин Х и Y приведены соответственно в таблицах:

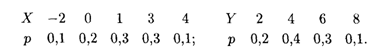
Найти дисперсию и среднее квадратическое отклонение слу­чайной величины Z = 2Х + 3Y.

Решение. Согласно свойствам 2 и 3 дисперсии (формулы (18.12) и (18.13)), имеем

Для вычисления дисперсий D(X) и D(Y) составляем соответ­ствующие таблицы — законы распределения случайных вели­чин Х2 и Y2:

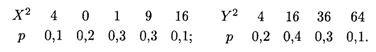
Отсюда получаем

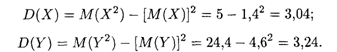
Искомые дисперсия и среднее квадратичное отклонение слу­чайной величины Z равны:

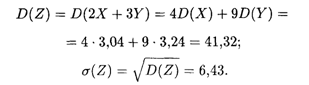
Пример 11. В условиях примера 8 найти математическое ожи­дание и среднее квадратическое отклонение прибыли при П = 1000, Р = 0,8, S = 100 тыс. р. и R = 30%.

Решение. Ставка ссудного процента удовлетворяет усло­вию, чтобы математическое ожидание прибыли было положи­тельным: 30 > 100 (1 - 0,8) / 0,8. Математическое ожидание при­были:

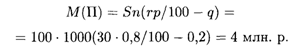
Среднее квадратическое отклонение прибыли:

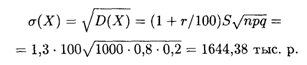
< Предыдущая		Следующая >