18.1.2. Биномиальное распределение

Пусть производится П независимых испытаний и в каждом из них событие А может либо появиться, либо не появиться. Пусть также вероятность Р появления события А в каждом ис­пытании постоянна (см. раздел 17.5). В качестве дискретной случайной величины Х рассмотрим число появления события А в этих П испытаниях. Очевидно, что X1 = 0, X2 = 1, X3 = 2, ..., Xn+1 = N. Вероятности этих возможных значений K даются фор­мулой Бернулли (см. формулу (17.16)):

Где Q = 1 - Р — вероятность противоположного события (непо­явление события А в одном испытании). Формула (18.2) пред­ставляет собой аналитическую форму закона распределения случайной величины (числа появления события А в N незави­симых испытаниях), которое называется Биномиальным. Этот закон получил свое название потому, что правая часть в (18.2) представляет собой общий член разложения бинома Ньютона (17.2). Таким образом, табличная форма биномиального закона с учетом формулы (18.2) имеет вид

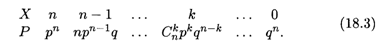
Можно показать, что сумма всех вероятностей второй стро­ки этой таблицы равна единице, т. е.

Пример 4. Банк выдает 5 кредитов. Вероятность невозвра­та кредита равна 0,2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вер­нувших кредит по окончании срока кредитования.

Решение. Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу 5 кредитов можно считать за 5 независимых событий. Вероятность невоз­врата K кредитов из 5 описывается биномиальным распределе­нием (18.2), где Р = 0,2, Q = 0,8, K принимает значения от нуля до 5. Искомая таблица закона распределения составляется, со­гласно (18.3), при П = 5:

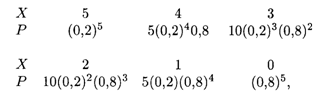
Или окончательно:

< Предыдущая		Следующая >