18.1.1. Дискретные случайные величины
Определение 4. Соответствие между отдельными возможными значениями и их вероятностями называется Законом распределения дискретной случайной величины.
Как и в случае функциональной зависимости, этот закон можно задать таблицей, аналитически (формулой) и графически. В случае табличного задания закона распределения дискретной случайной величины соответствующая таблица состоит из двух строк — первая указывает возможные значения, а вторая — их вероятности:
![]()
Поскольку в одном испытании случайная величина принимает только одно возможное значение, то события Х = х1, Х = х2, …, Х = XП образуют полную группу, т. е. сумма их вероятностей равна единице:
![]()
Если множество возможных значений Х дискретной случайной величины бесконечно, то соответствующий ряд вероятностей сходится и его сумма равна единице:
![]()
Пример 1. В денежной лотерее на 100 билетов разыгрывается один выигрыш в 20 р., два выигрыша по 10 р. и 10 выигрышей по 1 р. Найти закон распределения случайной величины Х возможного выигрыша на один билет.
Решение. Возможные значения X: X1 = 20, X2 = 10, X3 = 1, X4 = 0. Соответственно их вероятности равны: P1 = 0,01, Р2 = 0,02, Р3 = 0,1, Р4 = 1 - (P1 +P2 + Р3) = 1 - 0,13 = 0,87. Таким образом, искомый закон распределения имеет вид
![]()
Пример 2. Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение. Случайная величина Х — число стандартных деталей среди отобранных — может принимать 4 возможных значения: 0, 1, 2 и 3. Вероятность нахождения K стандартных изделий среди трех отобранных определяется формулой
![]()
Варьируя значения K от 0 до 3, получаем искомое распределение:
![]()
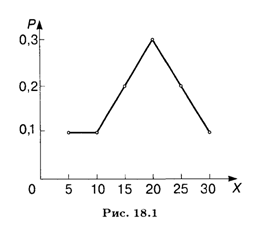
Пример 3. Вероятностный прогноз для величины Х — процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев — дан в виде закона распределения:
![]()
Найти вероятность того, что покупка акций будет более выгодна, чем помещение денег на банковский депозит под 36% годовых.
Решение. Прирост суммы на банковском депозите при условии 3% в месяц составит через 6 месяцев [(l,03)6 - l]100% = 19,4%. Вероятность того, что покупка акций выгоднее банковского депозита, определяется суммой вероятностей, соответствующих более высокому росту курса акций:
![]()
Закон распределения дискретной случайной величины можно изобразить графически, соединив в прямоугольной системе координат ХОР точки (хI, рi) отрезками прямых. Так, на рис. 18.1 показан закон распределения из примера 3. Такая фигура называется Многоугольником распределения.
| < Предыдущая | Следующая > |
|---|