18.1.3. Распределение Пуассона

Пусть в каждом из П производимых испытаний вероят­ность появления события А равна Р. Как мы знаем, для опреде­ления вероятности K появлений события А используется фор­мула Бернулли (18.2); при больших П пользуются асимптоти­ческой формулой Лапласа (17.17). Однако эта формула плохо подходит для случая, когда Р мало. Для случая малых значе­ний Р и больших значений П используется Асимптотическая формула Пуассона. Эта формула выведена при важном допу­щении, что произведение Пр является постоянной величиной, т. е. Пр = λ. Тогда вероятность того, что событие А наступит ровно K раз, дается формулой, которая представляет собой За­кон распределения Пуассона вероятностей массовых и редких событий:

Пример 5. На базу отправлено 10 000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0,0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия.

Решение. По условию задачи П = 10 000, Р = 0,0003, K = 4. Находим А, а затем по формуле (18.4) и искомую вероятность:

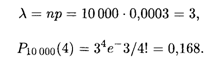
< Предыдущая		Следующая >