17.5. Схема независимых испытаний. Формула Бернулли

Определение 1. Если при проведении нескольких испытаний вероятность события А в каждом испытании не зависит от исходов других событий, то эти испытания называются Неза­висимыми относительно события А.

Будем рассматривать только такие независимые испыта­ния, в которых событие А имеет одинаковую вероятность. Пусть производится П независимых испытаний, в каждом из которых событие А может появиться с вероятностью Р. Тог­да вероятность противоположного события — ненаступления события А — также постоянна в каждом испытании и равна Q = 1 - P. В теории вероятностей представляет особый интерес случай, когда в П испытаниях событие А осуществится K раз и не осуществится П - k раз.

Вероятность этого сложного события, состоящего из П ис­пытаний, определяется Формулой Бернулли

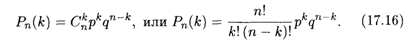
Пример 1. Монету бросают 6 раз. Найти вероятности того, что герб выпадет: 1) 2 раза, 2) не менее двух раз.

Решение. Вероятности выпадения любой из двух сторон монеты одинаковы, т. е. Р = Q = 0,5. 1) В этом случае П = 6, K = 2. Отсюда согласно формуле (17.16) получаем

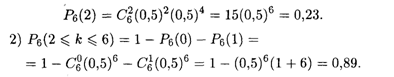
Пример 2. Вероятность покупки бракованного комплекта по­суды равна 0,1. Найти вероятность того, что из 7 купленных комплектов 5 будет без брака.

Решение. Вероятность покупки комплекта без брака Р = 0,9, Q = 0,1 — это дано по условию задачи. Тогда искомая вероятность находится по формуле (17.16):

Пример 3. Контрольный тест состоит из 4 вопросов. На каж­дый вопрос предлагается 4 варианта ответа, среди которых только один правильный. Найти вероятность правильного от­вета на два, три и четыре вопроса теста для неподготовленного человека (выбор ответа наудачу).

Решение. Искомые значения вероятности находятся по формуле Бернулли (17.16) с учетом того, что вероятность со­бытия А (правильный ответ) в каждом испытании (выбор от­вета на вопрос теста) равна 0,25, а Q = 0,75. Отсюда получаем:

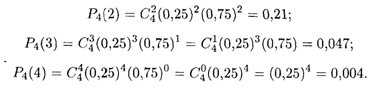
< Предыдущая		Следующая >