17.4.3. Формулы Байеса

Пусть события B1, B2, ..., Вп несовместны и образуют пол­ную группу, а событие А может наступить при условии появле­ния одного из них. События Bi называют Гипотезами, так как заранее неизвестно, какое из них наступит. Пусть произведено испытание и в результате появилось событие А. Тогда оказывается возможным определить условные вероятности гипотез Bi по следующим формулам:

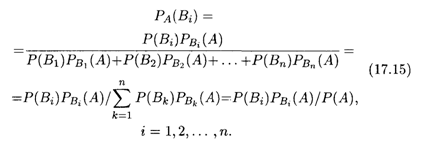
Формулы (17.15) называются Формулами Байеса, по имени их автора. Они позволяют оценить вероятность гипотезы Вi Во всех испытаниях, где наступает событие А. Иными слова­ми, зная вероятность Р(Вi) до проведения испытания, мы мо­жем переоценить ее после проведения испытания, в результате которого появилось событие А.

Пример 5. Вероятность изготовления изделия с браком равна 0,08. После изготовления все изделия подвергаются проверке, в результате которой изделия без брака признаются годными с вероятностью 0,95, а изделия с браком — с вероятностью 0,06. Найти долю изделий, выпущенных после проверки, а так­же вероятность того, что выпущенное после проверки изделие окажется без брака.

Решение. Независимые события (гипотезы), образующие полную группу, — это B1 (изделие без брака) и В2 (изделие с браком). Пусть событие А заключается в том, что при проверке изделие признается годным. Ответ на первый вопрос задачи дает формула (17.14):

Следовательно, после проверки признаются годными около 88% всех изготовленных изделий.

Ответ на второй вопрос задачи дает формула Байеса (17.15) при П = 2 и I = 1:

Иными словами, среди изделий, прошедших проверку, содер­жится 99, 5% изделий без брака.

Пример 6. В среднем из каждых 100 клиентов отделения бан­ка 60 обслуживаются первым операционистом и 40 — вторым операционистом. Вероятность того, что клиент будет обслужен без помощи заведующего отделением, только самим операци­онистом, составляет 0,9 и 0,75 соответственно для первого и второго служащих банка. Найти вероятность полного обслу­живания клиента первым операционистом.

Решение. Вероятность того, что клиент попадет к перво­му операционисту (событие B1), составляет 0,6, ко второму — 0,4 (событие В2). Искомая вероятность полного обслуживания клиента первым операционистом (событие А) определяется по формулам (17.14) и (17.15):

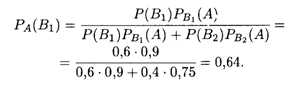
Иными словами, 64% клиентов, попавших на обслуживание к первому операционисту, будут обслужены им полностью.

< Предыдущая		Следующая >