17.4.2. Формула полной вероятности

Пусть события В1, В2, …, Вп несовместны и образуют пол­ную группу, т. е., согласно теореме 17.2, выполняется ра­венство

Пусть также событие А может наступить при условии появле­ния одного из событий ВI, причем известны как вероятности P(Bi), так и условные вероятности PBi(A) (I = 1, 2, ... , П). В таком случае формула для вероятности события А определя­ется следующей теоремой.

ТЕОРЕМА 6. Вероятность события А, появление которо­го возможно лишь при наступлении одного из несовместных событий Bi, образующих полную группу (i = 1, 2, ... ,п), рав­на сумме попарных произведений каждого из этих событий на соответствующую условную вероятность появления со­бытия А:

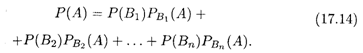
Пример 3. В двух урнах находятся белые и красные шары: в первой — 4 белых и 5 красных, во второй — 7 белых и 3 красных. Из второй урны наудачу взяли шар и переложили его в первую урну. Найти вероятность того, что наудачу взятый после этого из первой урны шар будет белым.

Решение. Перекладывание из второй урны в первую бело­го шара (событие В1) и красного шара (событие В2) образует полную группу независимых событий. Их вероятности соот­ветственно P(B1) = 0,7 и Р(В2) = 0,3. Условные вероятнос­ти извлечения из первой урны белого шара (событие А) при добавлении туда белого или красного шара из второй урны соответственно равны РB1(А) = 0,5 и РB2(А) = 0,4. Искомая вероятность находится по формуле (17.14) при П = 2:

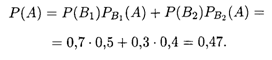
Пример 4. В двух ящиках находятся детали: в первом — 10 штук и из них 3 нестандартные, а во втором — 20 штук и из них 8 нестандартных. Из каждого ящика наудачу вынуто по одной детали, а потом из этих двух деталей наудачу взята одна. Найти вероятность того, что эта деталь окажется стандартной.

Решение. При первой выборке двух деталей возможны четыре случая, которые образуют полную группу независи­мых событий. События Bss, Bsn, Bns, Bnn соответствуют случаям изъятия: из первого и второго ящиков по стандарт­ной детали, из первого ящика — стандартной и из второ­го — нестандартной деталей, из первого ящика — нестан­дартной и из второго — стандартной, из первого и второго ящиков по нестандартной детали. В свою очередь события ВIk (I, K = S, N) представляют собой произведения независимых событий — изъятия из каждого ящика по детали, и потому их вероятности равны соответствующим произведениям веро­ятностей этих изъятий: P(Bss) = 0,7 • 0,6 = 0,42; P(Bsn) = 0,7 • 0,4 = 0,28; P(Bns) = 0,3 • 0,6 = 0,18; P(Bnn) = 0,3 • 0,4 = 0,12. Условные вероятности выборки из двух деталей стан­дартной, согласно перечисленным выше возможным случаям, равны:

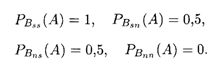
Теперь, согласно теореме 17.6 и формуле (17.14), получаем ис­комую вероятность события А:

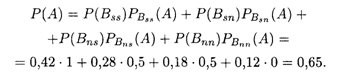
< Предыдущая		Следующая >