15.1.1. Матричная форма системы уравнений

Сведем коэффициенты при неизвестных в системе уравне­ний (15.1) в матрицу

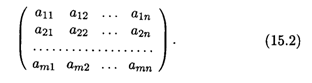
Эта матрица состоит из M строк и П столбцов и называет­ся Матрицей системы. Введем в рассмотрение две матрицы-столбца: матрицу неизвестных Х и матрицу свободных чле­нов В:

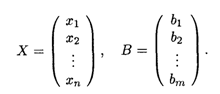
Х и В представляют собой векторы-столбцы, однако в целях единого подхода в рамках матричной алгебры удобнее тракто­вать их именно как матрицы, состоящие соответственно из П И M строк и одного столбца.

Тогда систему линейных уравнений (15.1) можно записать в матричной форме, поскольку размер матрицы А равен Т Х N, а размер Х — N х 1 и, значит, произведение этих матриц имеет смысл:

Произведение матриц АХ является, как и В, матрицей-столб­цом размером Т х 1, состоящей из левых частей уравнений сис­темы (15.1). Все уравнения этой системы вытекают из уравне­ния (15.3) в силу определения равенства двух матриц (п. 13.1).

Введем в рассмотрение еще одну матрицу; дополним мат­рицу системы А столбцом свободных членов и получим новую матрицу размером Т х (N + 1):

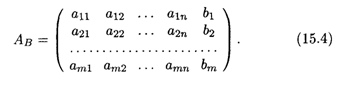
Матрица АВ называется Расширенной матрицей системы. Эта матрица играет важную роль в вопросе о разрешимости системы уравнений.

ТЕОРЕМА 1 (Кронекера-Капелли, критерий совместности системы). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу рас­ширенной матрицы системы.

Доказательство этой теоремы мы не приводим.

< Предыдущая		Следующая >