15.2.1. Методы решения систем линейных уравнений. Метод обратной матрицы и теорема Крамера

В этом разделе мы рассмотрим частный случай системы (15.1), когда число уравнений равно числу неизвестных, т. е. Т = N. Система уравнений имеет вид

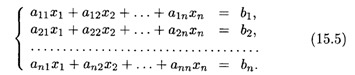
Составим квадратную матрицу А порядка N этой системы:

1. В матричной форме система уравнений (15.5) имеет вид

Где матрицы Х и В имеют размер N х 1. Пусть матрица систе­мы А является невырожденной, т. е. существует обратная мат­рица А-1. Умножив обе части этого уравнения слева на А-1, получаем решение системы (15.5) в матричной форме:

Вычисление обратной матрицы по заданной матрице А производится по довольно сложным формулам. В случае когда по­рядок N матриц А и А-1 достаточно велик, вычисление обрат­ной матрицы может быть очень громоздким.

2. Другой метод решения системы уравнений (15.5) основан на теореме Крамера. Составим определитель матрицы систе­мы А:

Который называется также Определителем системы. Заменим в этом определителе J-Й столбец на столбец свободных членов В, т. е. получим этой заменой другой определитель, который обозначим ΔJ:

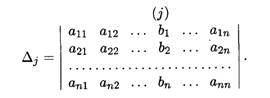
ТЕОРЕМА 2 (правило Крамера). Пусть Δ — Определитель матрицы системы А, а ΔJ — Определитель, полученный из определителя Δ Заменой j-го столбца столбцом свободных членов В. Тогда если Δ ≠ 0, То система линейных уравнений (15.5) Имеет единственное решение, определяемое по форму­лам

Формулы вычисления неизвестных (15.6) — решения сис­темы (15.5) — носят название Формул Крамера.

Пример 1. Найти решение системы уравнений

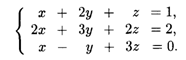
Решение. Составим и вычислим определители системы Δ и ΔJ (J = X, Y, Z):

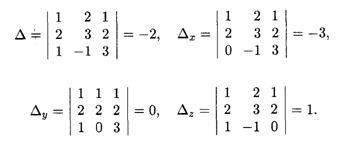
Определитель системы отличен от нуля, стало быть, она имеет единственное решение, которое вычисляется по форму­лам (15.6):

< Предыдущая		Следующая >