14.1.1. Основные свойства определителей

Из данного выше общего определения следуют основные свойства определителей.

1. Если некоторая строка или столбец определителя состо­ит из нулей, то определитель равен нулю.

Действительно, согласно общему определению, в каждое из N! слагаемых обязательно войдет сомножителем элемент нуле­вой строки (нулевого столбца).

2. При перестановке двух строк (столбцов) определитель меняет знак.

Это свойство легко проверяется на определителях второго и третьего порядков.

3. Определитель, содержащий две одинаковые строки (два одинаковых столбца), равен нулю.

Действительно, поменяв местами эти строки, получаем ΔN = -ΔN откуда и следует, что ΔN = 0.

4. Общий множитель любой строки (столбца) можно выне­сти за знак определителя.

5. Если каждый элемент некоторой строки (столбца) опре­делителя ΔN представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей, в каждом из которых: а) все строки (столбцы), за исключением указан­ной строки (столбца), совпадают с аналогичными строками (столбцами) определителя ΔN; б) на месте указанной строки (столбца) первый определитель содержит первые слагаемые, а второй определитель — вторые слагаемые данной строки (столбца) определителя ΔN.

Поясним это свойство на примере определителя третьего порядка:

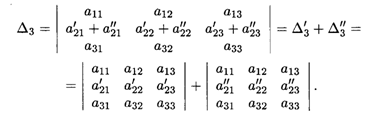
6. Определитель не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы дру­гой строки (столбца), умноженные на любое число.

Это свойство является следствием свойств 3-5.

7. При транспонировании матрицы определитель не меня­ется.

Из перечисленных свойств следует, что определитель ра­вен нулю, если по крайней мере одна из его строк (столбцов) является линейной комбинацией каких-либо других его строк (столбцов). Отсюда вытекает необходимое и достаточное усло­вие равенства нулю определителя. Определитель равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.

< Предыдущая		Следующая >