14.1. Определители. Операции над определителями и основные свойства

Любой квадратной матрице А порядка N ставится в соот­ветствие по определенному закону некоторое число, называе­мое Определителем, или Детерминантом, N-го порядка этой матрицы. Начнем с определителей второго и третьего поряд­ков.

Пусть дана матрица

Тогда ее определитель второго порядка вычисляется по фор­муле

Правило вычисления определителя второго порядка очевидно: из произведения элементов на главной диагонали вычитает­ся произведение элементов на второй диагонали матрицы А. Нетрудно видеть, что формула (14.1) представляет собой ал­гебраическую сумму двух попарных произведений элементов матрицы А, стоящих в разных строках и разных столбцах.

В дальнейшем мы не будем приводить матрицу, для кото­рой вычисляется определитель, так как в записи определителя содержатся все элементы соответствующей матрицы.

Определитель третьего порядка вычисляется по формуле

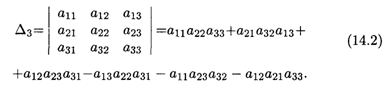
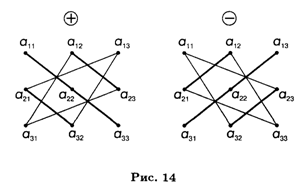
Правило вычисления определителя третьего порядка следу­ющее. Это алгебраическая сумма шести тройных произведе­ний элементов, стоящих в разных строках и разных столб­цах; со знаком плюс берутся произведения, сомножители кото­рых находятся на главной диагонали и в вершинах треугольников, чьи основания параллельны главной диагонали; со зна­ком минус — произведения, сомножители которых стоят на не главной диагонали и в вершинах треугольников с основани­ями, параллельными этой диагонали (рис. 14). Заметим, что каждое слагаемое в формуле (14.2) содержит по одному эле­менту из каждой строки и каждого столбца соответствующей матрицы.

Рассмотрим определитель N-го порядка

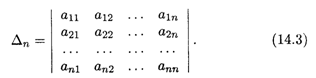
Теперь с учетом подмеченных выше закономерностей перейдем к определению для общего случая.

Определение 1. Определителем матрицы А N-го порядка на­зывается алгебраическая сумма N! произведений N-го порядка элементов этой матрицы, причем в каждое произведение вхо­дит по одному элементу из каждой строки и каждого столбца данной матрицы.

< Предыдущая		Следующая >