14.1.2. Миноры и алгебраические дополнения

Рассмотрим определитель N-го порядка (14.3). Выделим в нем какой-либо элемент АIj и вычеркнем I-Ю строку и J-Й стол­бец, на пересечении которых расположен этот элемент. Полу­ченный определитель (N - 1)-го порядка называется Минором Mij элемента Aij определителя ΔN.

Пример 1. Найти минор М32 определителя четвертого по­рядка

Решение. Минор М32 элемента A32 получается вычеркива­нием из данного определителя 3-й строки и 2-го столбца. По­лученный определитель 3-го порядка равен

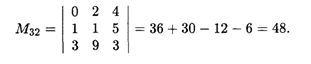
Определение 2. Алгебраическим дополнением элемента Aij определителя (14.3) называется число

Так, для приведенного выше примера алгебраическое до­полнение равно

Миноры и алгебраические дополнения играют важную роль в алгебре и ее приложениях. Одним из таких применений яв­ляется основополагающая теорема о способе вычисления опре­делителей.

ТЕОРЕМА 1. Определитель равен сумме произведений эле­ментов любой строки на их алгебраические дополнения:

Формула (14.4) называется Разложением определителя по I-Й строке. Доказательство этой теоремы мы опускаем. Анало­гичное утверждение имеет место и для разложения определи­теля по любому столбцу.

Формула (14.4) сводит вычисление определителя N-го по­рядка к вычислению N определителей (N - 1)-го порядка. Зная формулу (14.2) вычисления определителя 3-го порядка, мы, на­пример, можем найти определитель 4-го порядка путем разло­жения его на сумму алгебраических дополнений по формуле (14.4).

Пример 2. Вычислить определитель 4-го порядка

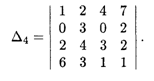
Решение. В принципе, разложить определитель можно по любой строке (столбцу), согласно формуле (14.4). Однако объ­ем вычислений можно существенно уменьшить, если выбрать такую строку (столбец), в которой побольше элементов равно нулю. Наиболее подходящей в нашем случае является вторая строка. Разложение по ней определителя имеет вил

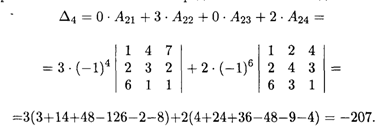
< Предыдущая		Следующая >