13.1.3. Умножение матриц

1. Умножение матриц — это специфическая операция, со­ставляющая основу алгебры матриц. Строки и столбцы мат­риц можно рассматривать как векторы-строки и векторы-стол­бцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.

Пусть даны матрица А размером Т Х п и матрица В разме­ром П х K. Будем рассматривать матрицу А как совокупность Т векторов-строк I размерности П каждый, а матрицу В — Как совокупность K векторов-столбцов J, каждый из которых содержит по П координат:

Векторы-строки матрицы А и векторы-столбцы матрицы В Показаны в записи этих матриц (13.3). Длина строки матри­цы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.

Определение 3. Произведением матриц А и В называется матрица С, элементы которой CIj равны скалярным произве­дениям векторов-строк I матрицы А на векторы-столбцы J Матрицы В:

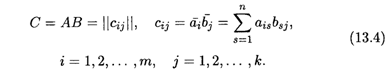
Произведение матриц А и В — матрица С — имеет размер Т х K, поскольку длина П векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих век­торов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скаляр­ные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как ска­лярные произведения второй вектор-строки матрицы А На все векторы-столбцы матрицы В и так далее. Для удобства за­поминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей:, т. е. размер матрицы С равен произведению оставшихся в отношении чисел: Т х K.

В операции умножения матриц есть характерная особен­ность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — Прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формиру­ющих элементы соответствующей матрицы, должны участво­вать векторы с одинаковым числом координат.

Если матрицы А И В квадратные размером N х N, то име­ет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у ис­ходных сомножителей. При этом в общем случае перемноже­ния матриц правило перестановочности не соблюдается, т. е. АВ ≠ ВА.

Рассмотрим примеры на умножение матриц.

Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:

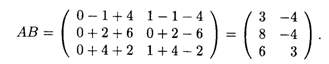
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.

Решение. Здесь мы найдем произведения данных матриц АВ и ВА:

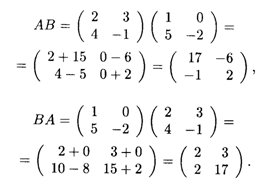
Как видно из результата, матрица произведения зависит от по­рядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.

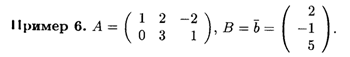
Решение. В данном случае матрица В представляет собой вектор-столбец, т. е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: век­тор-строка длины П представляет собой матрицу с одной стро­кой и П столбцами, а вектор-столбец высоты N — матрицу с N строками и одним столбцом. Размеры данных матриц соот­ветственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем

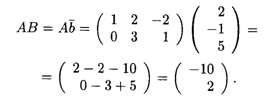
В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.

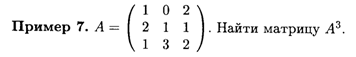
Решение. Путем последовательного умножения матриц находим

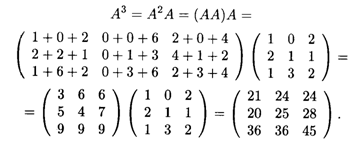
2. Свойства произведения матриц. Пусть А, В и С — мат­рицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следу­ющие свойства произведения матриц имеют место:

1) (АВ)С = А(ВС),

2) (А + В)С = AC + ВС,

3) А(В + С) = АВ + АС,

4) α(АВ) = (αА)В = А(αВ).

В п. 1 этого раздела введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т. е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадрат­ных матриц:

5) АЕ = А,

6) ЕА = А.

Иными словами, произведение любой матрицы на единич­ную матрицу, если оно имеет смысл, не меняет исходную мат­рицу.

< Предыдущая		Следующая >