13.1.2. Транспонирование матриц

Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка (или, что то же самое, замена столбцов матрицы на ее строки). Пусть дана исходная матрица А:

Тогда, согласно определению, транспонированная матрица А' имеет вид

Сокращенная форма записи операции транспонирования мат­рицы:

Пример 3. Пусть даны матрицы А и В:

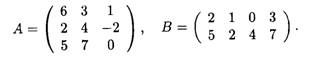
Тогда соответствующие транспонированные матрицы имеют вид

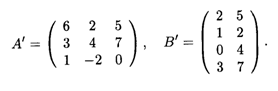
Нетрудно заметить две закономерности операции транспо­нирования матриц.

1. Дважды транспонированная матрица равна исходной матрице:

2. При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций, т. е. главная диагональ квадратной матрицы не меняется при транспонировании.

Важную роль в алгебре и ее приложениях играют Симмет­рические матрицы — квадратные матрицы, у которых элемен­ты, симметричные относительно главной диагонали, равны, т. е. Aij = Aji. Транспонирование таких матриц не меняет их вида, так что равенство

Также можно полагать определением симметрической мат­рицы.

< Предыдущая		Следующая >