13.1.1. Линейные операции над матрицами

1. Сумма матриц. Суммой матриц А и В одинакового раз­мера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В. Представим это в сокращенной записи. Пусть

Тогда сумма этих матриц С = А + В имеет вид

Пример 1. Пусть даны матрицы А и В:

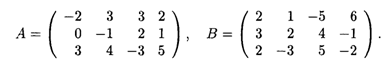
Тогда их суммой, согласно определению, является матрица

2. Умножение матрицы на действительное число. Произ­ведением матрицы А на действительное число α называется матрица, каждый элемент которой получен умножением соот­ветствующего элемента матрицы А на число α.

Пример 2. Пусть даны матрица А и число α:

Тогда произведением матрицы А на число является матрица

3. Приведем свойства операций суммирования матриц и произведения матрицы на число, непосредственно вытекающие из определения этих операций. Пусть А, В и С — матрицы, имеющие одинаковый размер, а α и β — некоторые действи­тельные числа. Тогда:

1) А + В = В + А,

2) (А + В) + С = А + (В + С),

3) α(А + В) =αА + αВ,

4) (α + β) A = αA + βA,

5) (αβ)А = (αA)β,

6) A + О = А, где О — нулевая матрица,

7) 0А = О.

< Предыдущая		Следующая >