12.3.2. Разложение вектора в ортогональном базисе

Рассмотрим базис пространства Rn, в котором каждый век­тор ортогонален остальным векторам базиса:

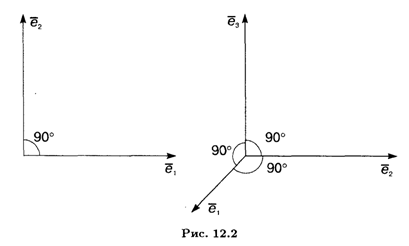
Ортогональные базисы хорошо известны и широко использу­ются на плоскости и в пространстве (рис. 12.2). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются по весьма простой про­цедуре, не требующей трудоемких вычислений.

Действительно, пусть требуется найти разложение произ­вольного вектора в ортогональном базисе (12.13). Составим разложение этого вектора с неизвестными пока координатами разложения в данном базисе:

Умножим обе части этого равенства, представляющие собой векторы, на вектор 1. В силу свойств 2 и 3 скалярного произ­ведения векторов имеем

Однако в силу взаимной ортогональности векторов базиса (12.13) все скалярные произведения векторов базиса, за исклю­чением первого, равны нулю, т. е. коэффициент α1 определяется по формуле

Умножая поочередно равенство (12.14) на другие базисные век­торы, мы получаем простую формулу для вычисления коэффи­циентов разложения вектора :

Нетрудно видеть, что соотношения (12.15) имеют смысл, по­скольку |I| ≠ 0.

Отметим особо частный случай ортогонального базиса, когда все векторы в (12.13) имеют единичную длину (|I| = 1), или нормированы по своей длине. В таком случае базис назы­вают Ортонормированным и координаты разложения (12.15) имеют наиболее простой вид:

< Предыдущая		Следующая >