12.3.1. Разложение вектора по базису. Представление вектора в произвольном базисе

Пусть система векторов

Является базисом, а вектор — их линейной комбинацией. Име­ет место следующая теорема.

ТЕОРЕМА 2. Разложение любого вектора в базисе, если оно существует, является единственным.

Доказательство. Предположим, что вектор может быть представлен в виде линейной комбинации векторов (12.9) двумя способами:

Где наборы чисел αI и βi, среди которых обязательно есть не­нулевые значения, не совпадают. Вычитая одно равенство из другого, имеем

Мы получили, что линейная комбинация векторов системы (12.9), в которой не все коэффициенты равны нулю (в силу несовпадения αi и βi), равна нулю, т. е. данная система оказа­лась линейно зависимой, что противоречит условию теоремы. Полученное противоречие доказывает теорему.

Стало быть, в произвольном базисе пространства Rn

Любой вектор этого пространства обязательно представим в виде разложения по базисным векторам:

Причем это разложение является Единственным для данного базиса. Коэффициенты разложения

Называются Координатами вектора в базисе (12.10), и, как следует из сказанного, этот набор единственный для любого вектора из Rn в данном базисе.

Задача нахождения коэффициентов разложения в случае произвольного базиса (12.10) является, вообще говоря, непро­стой. Нужно приравнять соответствующие координаты линей­ной комбинации векторов слева и координаты вектора в (12.11). Пусть базисные векторы и вектор заданы в следующей координатной форме:

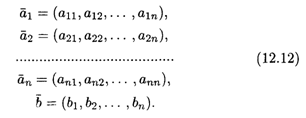
Выполнение процедуры, описанной выше, приводит к Системе п линейных уравнений относительно П неизвестных координат разложения вектора в базисе (12.10):

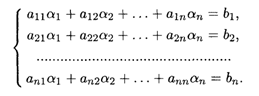
Такие системы уравнений и методы их решения представляют отдельные разделы линейной алгебры; они будут рассмотрены в следующих главах.

< Предыдущая		Следующая >