11.1.3. Неоклассическая модель роста

Пусть Y = F (K, L) — национальный доход, где F — одно­родная производственная функция первого порядка (F (TK, TL) = TF (K, L)), К — объем капиталовложений (про­изводственных фондов), L — объем затрат труда. Введем в рассмотрение величину фондовооруженности K = K/L, тогда производительность труда выражается формулой

Целью задачи, рассматриваемой в этом разделе, является описание динамики фондовооруженности или представление ее как функции от времени T. Поскольку любая модель базирует­ся на определенных предпосылках, нам нужно сделать некото­рые предположения и ввести ряд определяющих параметров. В данном случае будем полагать, что выполнены следующие предположения.

1. Имеет место естественный прирост во времени трудовых ресурсов:

2. Инвестиции расходуются на увеличение производствен­ных фондов и на амортизацию, т. е.

Где β — норма амортизации.

Тогда если L — норма инвестиций, то I = LY = К' + βК, или

Из определения фондовооруженности K вытекает, что

Дифференцируя это равенство по T, имеем

Подставив в это соотношение выражения (11.15) и (11.16), по­лучаем уравнение относительно неизвестной функции K

Где функция F(K) определена по формуле (11.14).

Полученное соотношение (11.17) представляет собой нели­нейное дифференциальное уравнение первого порядка с раз­деляющимися переменными (которое является автономным). Выделим стационарное решение этого уравнения; из условия K' = 0 следует, что

Т. е. K = const — постоянная величина, являющаяся корнем этого нелинейного алгебраического уравнения.

Рассмотрим конкретную задачу: для производственной функции F(K, L) = Найти интегральные кривые урав­нения (11.17) и стационарное решение. Из (11.14) следует, что F(k) =, и тогда уравнение (11.17) имеет вид

Стационарное решение этого уравнения следует из равенства

Откуда получаем ненулевое частное решение уравнения (11.17): KSt = I2/(α + β)2.

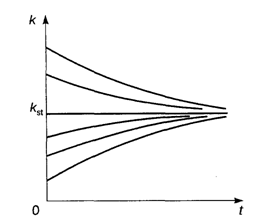
Рис. 11.4

Дифференциальное уравнение (11.17) решаем методом раз­деления переменных:

Интегрируя это уравнение с заменой переменной = Z, по­лучаем его общее решение в окончательном виде:

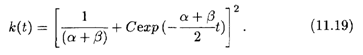
Семейство интегральных кривых сходится сверху и снизу к стационарному решению (рис. 11.4): т. е. K KSt при T . Следовательно, при неизменных входных параметрах задачи L, α и β функция фондовооруженности в данном случае устой­чиво стремится к стационарному значению независимо от на­чальных условий. Такая стационарная точка K = KSt является точкой устойчивого равновесия.

< Предыдущая		Следующая >