11.1.2. Динамическая модель Кейнса

Рассмотрим простейшую балансовую модель, включаю­щую в себя основные компоненты динамики расходной и до­ходной частей экономики. Пусть Y(T), E(T), S(T), I(T) — со­ответственно национальный доход, государственные расходы, потребление и инвестиции. Все эти величины рассматривают­ся как функции времени T. Тогда справедливы следующие со­отношения:

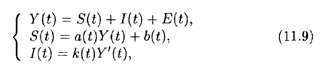
Где A(T) — коэффициент склонности к потреблению (0 < А(T) < 1), B(T) — автономное (конечное) потребление, K(T) — норма аксе­лерации. Все функции, входящие в уравнения (11.9), положи­тельны.

Поясним смысл уравнений (11.9). Сумма всех расходов дол­жна быть равной национальному доходу — этот баланс отра­жен в первом уравнении. Общее потребление состоит из внут­реннего потребления некоторой части национального дохода в народном хозяйстве и конечного потребления — эти составля­ющие показаны во втором уравнении. Наконец, размер инвес­тиций не может быть произвольным: он определяется произве­дением нормы акселерации, величина которой характеризуется уровнем технологии и инфраструктуры данного государства, на предельный национальный доход.

Будем полагать, что функции A(T), B(T), K(T) и E(T) зада­ны — они являются характеристиками функционирования и эволюции данного государства. Требуется найти динамику на­ционального дохода, или Y как функцию времени T.

Подставим выражения для S(T) из второго уравнения и для I(T) из третьего уравнения в первое уравнение. После приве­дения подобных получаем дифференциальное неоднородное ли­нейное уравнение первого порядка для функции Y(T):

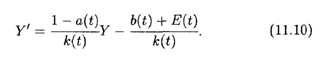
Согласно п. 9.4, существует достаточно сложная формула об­щего решения этого уравнения. Мы проанализируем более про­стой случай, полагая основные параметры задачи А, B и K по­стоянными числами. Тогда уравнение (11.10) упрощается до линейного дифференциального уравнения первого порядка с постоянными коэффициентами:

Как известно, общее решение неоднородного уравнения есть сумма какого-либо его частного решения и общего решения со­ответствующего однородного уравнения. В качестве частного решения уравнения (11.11) возьмем так называемое Равновес­ное решение, когда Y’ = 0, т. е.

Нетрудно видеть, что эта величина положительна. Общее ре­шение однородного уравнения дается формулой , так что общее решение уравнения (11.11) имеет вид

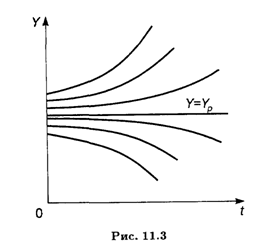
Интегральные кривые уравнения (11.11) показаны на рис. 11.3. Если в начальный момент времени Y0 < Yp , то С = Y0 — Yp < 0 и кривые уходят вниз от равновесного решения (11.12), т. е. национальный доход со временем пада­ет при заданных параметрах задачи А, B, k и Е, так как показатель экспоненты в (11.13) положителен. Если же Y0 > Yp, то С > 0 и национальный доход растет во времени — интегральные кривые уходят вверх от равновесной прямой Y = YР.

Согласно классификации п. 9.3, уравнение (11.11) является автономным; точка Y = Yp представляет собой точку неустой­чивого равновесия.

< Предыдущая		Следующая >