11.1.1. Рост выпуска в условиях конкуренции

В этой модели мы снимем предположение о ненасыщае­мости рынка. Пусть Р = Р(Q) — убывающая функция, т. е. с увеличением объема продукции на рынке цена на нее пада­ет: DP/DQ < 0. Теперь из формул (11.1)-(11.3) мы получаем нелинейное дифференциальное уравнение первого порядка относительно Q С разделяющимися переменными:

Поскольку все сомножители в правой части этого уравнения положительны, то Q' > 0, т. е. функция Q(T) возрастающая.

Характер возрастания функции определяется ее второй производной. Из уравнения (11.5) получаем

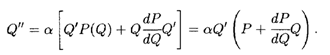
Это равенство можно преобразовать, введя эластичность спроса

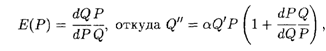
Или, так как < 0, а значит, и Е < 0, окончательно получаем

Из уравнения (11.6) следует, что Q" > 0 при эластич­ном спросе, т. е. когда |Е| > 1, и график функции Q(T) име­ет направление выпуклости вниз, что означает прогрессирую­щий рост. При неэластичном спросе |Е| < 1, и в этом случае Q" < 0 — направление выпуклости функции Q(T) вверх, что означает замедленный рост (насыщение).

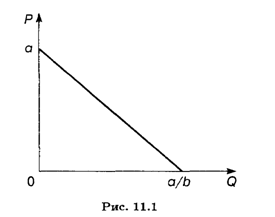
Для простоты примем зависимость P(Q) в виде линейной функции

(рис. 11.1). Тогда уравнение (11.5) имеет вид

Откуда

Из соотношений (11.7) и (11.8) получаем: Q' = 0 при Q = 0 и при Q = а/b, Q" > 0 при Q < а /(2B) и Q" < 0 при Q > А/(2B); Q = A/(2B) — точка перегиба графика функции Q = Q(T). Приведенный на рис. 11.2 график этой функции (од­ной из интегральных кривых дифференциального уравнения (11.7)) носит название Логистической кривой.

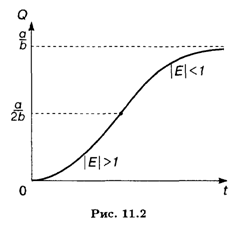
Аналогичные кривые характеризуют и другие процессы, например размножение бактерий в ограниченной среде обита­ния, динамику эпидемий внутри ограниченной общности био­логических организмов и др.

< Предыдущая		Следующая >