10.2. Уравнения, допускающие понижение порядка

Существуют три вида уравнения (10.2), которые при помо­щи замены переменной (искомой функции) сводятся к уравне­ниям первого порядка.

1. Уравнение вида

Введем новую функцию Z(X) путем замены Z(X) = У'. Тогда исходное уравнение второго порядка преобразуется в неполное уравнение первого порядка: Z' = F(X), решением которого яв­ляется функция Z(х) = F(X) Dx + С1. Поскольку Z(X) = у', то повторным интегрированием находим общее решение уравне­ния (10.4):

Где С1 и С2 — произвольные постоянные.

2. Уравнение вида

Т. е. уравнение не содержит в явном виде у. Как и в преды­дущем случае, положим Z(X) = у'. Тогда получаем уравнение первого порядка общего вида Z' = F(X, Z). Найдя общее реше­ние этого уравнения Z = φ(X, C1), повторным интегрированием получим искомое общее решение уравнения (10.5):

Где С1 и С2 — произвольные постоянные.

3. Уравнение вида

Т. е. уравнение не содержит независимой переменной X. Здесь мы вводим новую функцию, зависящую от У, полагая Z(Y) = У'. Тогда, поскольку по правилу дифференцирования сложной функции

То уравнение (10.6) преобразуется в дифференциальное урав­нение первого порядка относительно функции Z(Y):

Пусть общее решение этого уравнения Z = φ(у, С1). Тогда об­ратной заменой получаем неполное уравнение первого порядка относительно функции У(х)

Из которого методом разделения переменных получаем функ­циональное соотношение для определения общего решения уравнения (10.6):

Где С1 и C2 — произвольные постоянные.

Рассмотрим два примера решения дифференциальных уравнений второго порядка.

Решение. Это уравнение вида (10.5), поскольку оно не со­держит в явном виде У. Заменой Z(X) = у' приведем его к уравнению первого порядка = -Xz2, откуда имеем Z = , Или У' = . Интегрируя это уравнение, получаем общее решение исходного уравнения:

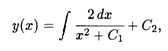
Где С1 и С2 — произвольные постоянные. В зависимости от вы­бора знака С1 интеграл в правой части этого равенства (обо­значим его через I) может иметь разные выражения:

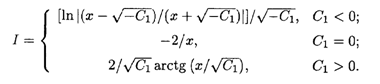
Решение. Это уравнение вида (10.6), т. е. оно не содержит явно независимой переменной Х. Заменой Z(Y) = У' сведем его к уравнению первого порядка

Первое решение этого уравнения Z = 0, или У = С, где С — по­стоянная величина. Сокращая после этого обе части уравнения на Z, получаем — Z = 0. Решение этого уравнения методом разделения переменных У и Z дает Z = С1Ey. Наконец, обратная замена приводит к уравнению первого порядка

Разделение переменных X и У приводит к общему решению ис­ходного уравнения: E-ydy = C1Dx, откуда E-y = С1Х + С2, или окончательно

Где С1 и С2 — произвольные постоянные. Нетрудно видеть, что это решение включает в себя и решение У = С, указанное выше (при С1 = 0, С2 ≠ 0).

Далее мы рассмотрим наиболее употребимый в математи­ческих приложениях вид дифференциальных уравнений второ­го порядка.

< Предыдущая		Следующая >