10.1. Дифференциальные уравнения второго порядка. Основные понятия теории

Определение 1. Дифференциальным уравнением Второго по­рядка называется уравнение вида

Где Х — независимая переменная, У — искомая функция, У' и У" — соответственно ее первая и вторая производные.

Примеры дифференциальных уравнений второго порядка:

Будем рассматривать уравнения, которые можно записать в виде, разрешенном относительно второй производной:

Как и в случае уравнения первого порядка, решением урав­нения (10.1) называется функция У = φ(X), определенная на некотором интервале (А, B), которая обращает это уравнение в тождество. График решения называется Интегральной кривой. Имеет место теорема существования и единственности реше­ния уравнения второго порядка.

ТЕОРЕМА 1 (теорема Коши). Пусть функция f(x, у, у') и ее частные производные и , непрерывны в некоторой обла­сти D пространства переменных (x, у, у'). Тогда для любой внутренней точки М0(х0, у0, у'0) этой области существует единственное решение уравнения (10.2), удовлетворяющее ус­ловиям:

Геометрический смысл этой теоремы (ее доказательство мы не приводим) заключается в том, что через заданную точку (X0, Y0) на координатной плоскости Оху проходит Единствен­ная интегральная кривая с заданным угловым коэффициентом Y0' касательной (рис. 10.1).

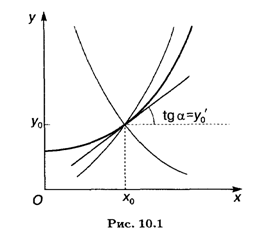
Условия (10.3) называются Начальными условиями, а зада­чу отыскания решения уравнения (10.2) по заданным началь­ным условиям называют Задачей Коши.

Общим решением уравнения (10.2) в некоторой области D Называется функция У = φ(х, С1, С2), если она является реше­нием этого уравнения при любых постоянных величинах С1 и C2, которые могут быть определены единственным образом при заданных начальных условиях (10.3). Частным решением Уравнения (10.2) называется общее решение этого уравнения при фиксированных значениях постоянных С1 и C2: У = φ(х, С10, С20).

Рассмотрим для пояснения уравнение У" = 0. Его общее решение получается при двухкратном интегрировании этого уравнения:

Где С1 и C2 — произвольные постоянные. Это решение пред ставляет собой семейство прямых, проходящих в произвольных направлениях, причем через каждую точку плоскости Охy Проходит бесконечное число таких прямых. Поэтому для выделения частного решения, проходящего через заданную точку (х0, y0), следует задать еще и угловой коэффициент прямой, совпадающей в данном случае со своей касательной. Например, найдем частное решение, удовлетворяющее начальным условиям

Т. е. нужно найти прямую, проходящую через точку M (l, 2), с угловым коэффициентом, равным единице. Подстановка на­чальных условий в общее решение уравнения приводит к сис­теме двух линейных уравнений относительно постоянных С1 и C2

Откуда С1 = 1, C2 = 1. Таким образом, искомое частное реше­ние — это прямая У = х + 1.

< Предыдущая		Следующая >