09.2. Уравнения с разделяющимися переменными

Определение 5. Дифференциальное уравнение вида

Где F1(X) и F2(Y) — непрерывные функции, называется уравне­нием с разделяющимися переменными.

Подчеркнем, что правая часть уравнения представляет со­бой произведение, в котором один сомножитель зависит только от Х, а другой — только от У. Метод решения такого вида урав­нений носит название Разделения переменных. Запишем производную У' в ее эквивалентной форме как отношение дифферен­циала функции к дифференциалу независимой переменной , умножим обе части уравнения (9.3) на Dx и поделим обе его части на F2(Y), полагая, что F2(У) ≠ 0; получаем

В этом уравнении переменная У входит в левую часть, а пе­ременная Х — только в правую, т. е. переменные разделены. Пусть У = φ(X) является решением уравнения (9.3), тогда при подстановке этого решения в уравнение (9.4) получаем тож­дество: два дифференциала равны друг другу, только в правой части дифференциал выражен через независимую переменную X, а в левой части — через функцию У. Поскольку дифференци­алы равны, то их неопределенные интегралы различаются на постоянную величину, т. е., интегрируя слева по переменной У, А справа по переменной Х, получаем

Где С — произвольная постоянная.

Рассмотрим примеры решения уравнений методом разде­ления переменных.

Пример 1. Ху' — у = 0, найти частное решение при начальных условиях У0 = 2 при X0 = -4.

Решение. Разделим переменные, для чего перенесем У в правую часть, поделим обе части полученного уравнения на Ху и умножим их на Dx; получим

Интегрируя обе части этого уравнения (правую по X, а левую по У), имеем

Где С — произвольная постоянная. При потенцировании полу­чаем

Что эквивалентно уравнению У = ±Сх, или У = С1Х. Получен­ная функция представляет семейство интегральных кривых. Для выделения частного решения при указанных начальных условиях подставим в эту формулу Х = -4 и У = 2, откуда получим значение для С: С = -1/2. Окончательно частное решение имеет вид

Пример 2. У' = х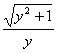, найти частное решение, проходящее через точку (0,1).

Решение. Разделяя переменные, получаем уравнение в дифференциалах

Интегрируя, имеем

Где С — произвольная постоянная величина. После интегриро­вания (интеграл в правой части берется при помощи замены переменной) имеем уравнение семейства интегральных кривых

Выделение частного решения, проходящего через точку (0, 1), приводит к определению произвольной постоянной: С =, т. е. эта кривая описывается уравнением (с учетом выбора знака)

< Предыдущая		Следующая >