09.2. Геометрический смысл уравнения первого порядка

Рассмотрим уравнение У' = F(X,Y). Пусть У = φ(X) — Его решение, график которого представляет собой непрерыв­ную интегральную кривую, причем в каждой ее точке сущест­вует касательная. Из дифференциального уравнения следует, что угловой коэффициент касательной к интегральной кривой в каждой ее точке равен правой части этого уравнения. Сле­довательно, уравнение первого порядка задает угловой коэф­фициент У' касательной к интегральной кривой как функцию двух переменных. Если каждой точке (X, У) сопоставить отрезок, направленный под углом наклона α = arctg (F (X, Y)) к оси Ох, то мы получим Поле направлений данного уравнения. В этом и заключается геометрический смысл дифференциально­го уравнения первого порядка.

Поле направлений позволяет проанализировать решение дифференциального уравнения и даже приближенно построить интегральные кривые.

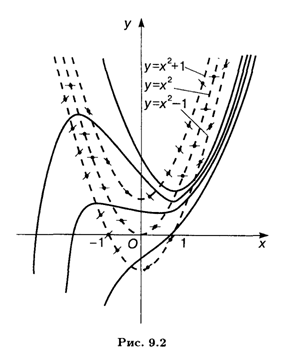
Пример 1. Построить поле направлений уравнения Y' = X2 - Y.

Решение. Нетрудно видеть, что правая часть этого урав­нения удовлетворяет условиям теоремы Коши единственности и существования решения при любых X и У, т. е. интегральные кривые заполняют всю плоскость Оху. Найдем линии, на ко­торых наклон направлений одинаков, — так называемые Изоклины. Так, если У' = 0, то имеем X2 - У = 0, т. е. на параболе У = X2 касательные к интегральным кривым горизонтальны (короткие черточки на рис. 9.2). При У' = 1 имеем Х2 — у = 1, т. е. касательные к интегральным кривым направлены под уг­лом 45° к оси Ох на параболе У = х2 - 1. Наконец, на параболе У = X2 + 1 угол наклона касательных равен 135°. По полю на­правлений можно приближенно восстановить ход интеграль­ных кривых (сплошные линии).

< Предыдущая		Следующая >