08.5.2. Оптимальное распределение ресурсов

Рассмотрим типичную задачу оптимального распределе­ния ресурсов на примере функции выпуска И = а0Ху2 при до­пущении, что функция затрат на ресурсы X и У линейна, т. е. имеет вид И = Р1Х+Р2У, где P1 и Р2 — соответствующие цены на эти факторы.

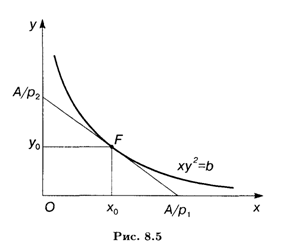
В точке F(X0, Y0), определяющей оптимальное определение ресурсов, линии уровня функций выпуска и затрат касают­ся (рис. 8.5). Эти линии определяются соответственно уравне­ниями A0Xy2 = C, Р1Х + Р2У = А, или У = (B/X)1/2, У = —(Р1/Р2)х + А/Р2, где C > 0 и A > 0 — постоянные числа, B =C/A0. Условие касания этих линий дается уравнением

Из этого уравнения определяется значение X0 = B1/3(P2/2P1)2/3. Тогда из уравнения линии уровня функции выпуска определя­ется значение У0 = (B/X0)1/2 = B1/3(2P1/P2)1/3. Отсюда полу­чаем, что оптимальное распределение ресурсов Х0/у0 должно быть произведено в отношении Р2 : 2P1.

< Предыдущая		Следующая >