08.4.1. Локальный экстремум функции нескольких переменных. Определение и необходимые условия существования локального экстремума

Пусть функция Z = F(X, Y) определена на множестве {М}, а М0 (X0, У0) — некоторая точка этого множества.

Определение. Функция Z = F(X, у) имеет в точке М0 локаль­ный максимум (минимум), если существует такая окрестность точки M0, принадлежащая {М}, что для любой точки М(х, у) Из этой окрестности выполняется неравенство F(M) ≤ F(M0) (F(М) ≥ F(М0)); для случая функции трех и более переменных локальный экстремум определяется аналогично.

Согласно данному определению локального экстремума (минимума или максимума) полное приращение функции Z = F(M) — F(М0) удовлетворяет одному из условий в окрест­ности точки M0:

ΔZ ≤ 0, если M0 — точка локального максимума;

ΔZ ≥ 0, если M0 — точка локального минимума.

Теперь установим необходимые условия существования ло­кального экстремума.

ТЕОРЕМА 2. Если функция z = F(X, у) имеет в точке M0 (X0, Y0) Локальный экстремум и частные производные пер­вого порядка, то все эти частные производные равны нулю:

Для случая функции двух и более переменных необходи­мое условие существования локального экстремума имеет вид, аналогичный (8.10); все частные производные первого порядка должны обращаться в нуль в точке M0.

Следует особо отметить, что условия (8.10) не являются достаточными условиями экстремума. Например, для функции Z = Х2 — У2 частные производные равны нулю в точке O(0, 0), однако в этой точке функция (которая является уравнением ги­перболического параболоида) не имеет экстремума: F(0, 0) = 0, но в любой окрестности точки О есть значения функции как положительные, так и отрицательные.

Точки, в которых выполняются условия (8.10), называются точками возможного экстремума, или Стационарными точ­ками.

Рассмотрим задачи на отыскание возможного экстремума функций.

Ррешение. Согласно условиям (8.10) имеем = 0 и = 0, откуда получаем систему двух алгебраических урав­нений с двумя неизвестными

Решение этой системы Х = 1, У = 2, т. е. точка с координа­тами (1, 2) является стационарной для данной функции двух переменных.

Решение. По условию (8.10) все три первые частные про­изводные функции равны в этой точке нулю, откуда получаем систему трех линейных алгебраических уравнений с тремя не­известными

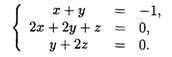
Решение этой системы дает единственную стационарную точ­ку возможного экстремума: (3, -4, 2).

< Предыдущая		Следующая >