08.3.3. Частные производные высших порядков

Частные производные первого порядка от функции двух и более переменных также представляют собой функции не­скольких переменных, и их можно также продифференциро­вать, т. е. найти частные производные от этих функций. Так, для функции двух переменных вида Z = F(X, У) возможны че­тыре вида частных производных второго порядка:

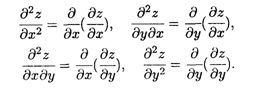
Частные производные, в которых дифференцирование произво­дится по разным переменным, называются Смешанными произ­водными. Аналогичным образом для функций нескольких пе­ременных определяются частные производные более высоких порядков.

Рассмотрим два примера нахождения частных производ­ных второго порядка для функции двух переменных.

Решение. Последовательно дифференцируя, получаем

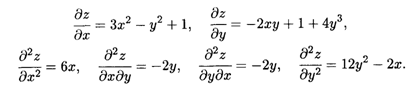
Решение. По правилам дифференцирования произведения имеем

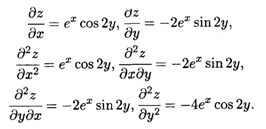
В рассмотренных примерах смешанные производные оказа­лись равными друг другу, хотя это бывает и не всегда. Ответ на вопрос о независимости смешанных вторых производных от порядка дифференцирования функции двух переменных дает следующая теорема.

ТЕОРЕМА 1. Если функция Z = F(X, У) дважды дифферен­цируема в точке М0(X­0, Y0), ТO ее Смешанные производные в этой точке равны.

< Предыдущая		Следующая >