08.3.2. Градиент

Рассмотрим функцию трех переменных И = F(X, у, Z), диф­ференцируемую в некоторой точке M(X, Y, Z).

Определение 1. Градиентом функции И = F(X, У, Z) называ­ется вектор, координаты которого равны соответственно частным производным в точке М.

Для обозначения градиента функции используется символ

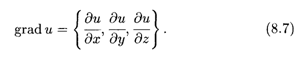
Аналогично в случае функции двух переменных И = F(X, У) Имеем

Градиент функции характеризует направление и величину максимальной скорости возрастания этой функции в точке.

Для определения геометрического смысла градиента функ­ции введем понятие поверхности уровня. Это понятие анало­гично понятию линии уровня, рассмотренному в п. 8.2.

Определение 2. Поверхностью уровня функции И = F(X, у, z) Называется поверхность, на которой эта функция сохраняет по­стоянное значение

В курсе математического анализа доказывается, что градиент в данной точке ортогонален к этой поверхности.

В случае функции двух переменных все сказанное выше остается в силе, только вместо поверхности уровня будет фи­гурировать линия уровня. Рассмотрим некоторые примеры.

Пример 5. Найти градиент и его модуль функции Z = в точке М (0, 1).

Решение. По формуле (8.8) имеем для функции двух пе­ременных

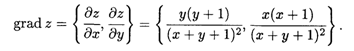
При Х = 0 и У = 1 получаем

Пример 6. Найти градиент и его модуль функции И = x2 + у2 - z2 в точке М (1, 1, -2).

Решение. По формуле (8.7) имеем

Подставляя в это выражение координаты точки М, полу­чаем

Пример 7. Найти поверхности уровня функции U = Х2 — 2Х + у2 + 2У — Z.

Решение. Согласно определению поверхности уровня (8.9) имеем

Где С = С + 2. Следовательно, поверхностями уровня данной функции являются параболоиды вращения с осью Х = 1, У = -1, параллельной оси Oz, вершины которых лежат в точках с ко­ординатами (1, -1, -С).

< Предыдущая		Следующая >