08.3.1. Частные производные функции нескольких переменных. Частные производные первого порядка

Пусть функция двух переменных Z = F(X, у) определена в некоторой окрестности точки М(X, У) евклидова пространства Е2. Частная производная функции Z = F(X, У) по аргументу X является обыкновенной производной функции одной перемен­ной Х при фиксированном значении переменной У и обознача­ется как

Аналогичным образом определяется частная производная функции F(X, У) по переменной У в точке М, обозначаемая как

Функция, имеющая частные производные, называется Диффе­ренцируемой.

Совершенно аналогично определяются частные производ­ные функций трех и более переменных. Частная производная функции нескольких переменных характеризует скорость ее изменения по данной координате при фиксированных значени­ях других координат.

Найти частные производные следующих функций.

Решение. Дифференцируем функцию Z = F(X, Y) сначала по Х, полагая У фиксированной величиной, потом повторяем эту же процедуру, меняя роли X и У. Получаем

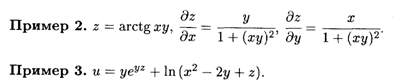
Ррешение. Частные производные этой функции трех пере­менных выражаются следующими формулами:

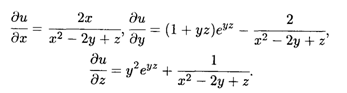
Пример 4. Найти предельные показатели продукции Q при изменении одного из факторов: затрат капитала К или вели­чины трудовых ресурсов L — по функции Кобба—Дугласа

Решение. Частные производные этой функции

Дают решение сформулированной выше задачи. Очевидно, что в функции Кобба—Дугласа показатели степеней α и l — α пред­ставляют собой соответственно коэффициенты эластичности EK(Q) и EL(Q) по каждому из входящих в нее аргументов.

< Предыдущая		Следующая >