08.2.3. Некоторые виды функций нескольких переменных

Рассмотрим примеры функций нескольких переменных и найдем их области определения.

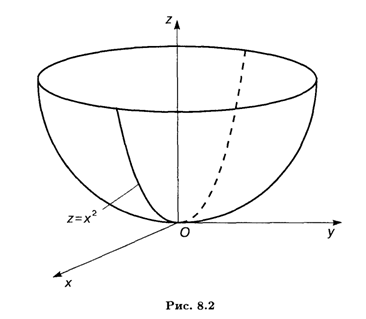
Решение. Это поверхность в евклидовом пространстве Е3. Областью определения этой функции является все множест­во точек плоскости Оху. Область значений этой функции — промежуток [0, ). Данная функция представляет собой пара­болоид вращения (рис. 8.2): в вертикальных сечениях этой поверхности плоскостями Oxz и ОуZ получаются соответственно параболы Z = х2 и Z = у2.

Решение. Это поверхность в евклидовом пространстве Е3. Область определения данной функции — все множество точек евклидова пространства Е2 или плоскости Оху. Эта функция является так называемым эллиптическим конусом с вершиной в начале координат O(0, 0, 0); приведенная формула суммирует две функции, задающие две его симметричные относительно плоскости Оху части (рис. 8.3):

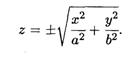
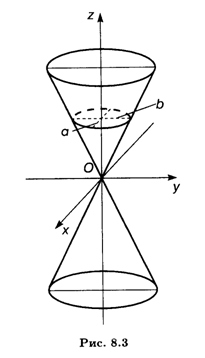
Приведем теперь наиболее часто встречающиеся в различ­ных приложениях виды функций нескольких переменных.

1. Уравнение вида

Называется Общим уравнением плоскости в системе коорди­нат Oxyz. Вектор = (А, В, С) перпендикулярен плоскости (8.4); он называется Нормальным вектором этой плоскости. Ес­ли известно, что плоскость проходит через некоторую точку M0(X0, Y0, Z0), то она может быть задана уравнением

Например, составить уравнение плоскости с перпендику­лярным вектором = (1, 2, -1), проходящей через точку М0 (2, 1, 1), Согласно формуле (8.5) имеем

2. Функция Кобба—Дугласа — производственная функция, показывающая объем выпуска продукции Q при затратах ка­питала К и трудовых ресурсов L. Для случая двух переменных она имеет вид

Где А > 0 — параметр производительности конкретно взятой технологии, 0 < α < 1 — доля капитала в доходе.

08.2.4. Линии уровня

Понятие линии уровня широко используется прежде всего в геодезии, картографии, при составлении синоптических карт, а также при описании различных физических полей (темпера­тура, давление и пр.).

Определение 2. Линией уровня функции двух переменных Z = F(X, Y) называется плоская кривая, получаемая при пе­ресечении графика этой функции плоскостью Z = С, где С — Постоянная величина, параллельной координатной плоскости Оху.

Обычно линии уровня, соответствующие различным зна­чениям постоянной величины С, проецируются на одну плос­кость, например на координатную плоскость Оху; тогда их удобно анализировать и с их помощью исследовать сложный характер поверхности, описываемой функцией Z = F(X, У).

Таким образом, можно сказать, что линии уровня функции Z = F(X, У) — это семейство кривых на координатной плоскос­ти Оху, описываемое уравнениями вида

Обычно берут арифметическую прогрессию чисел Ci с по­стоянной разностью H; тогда по взаимному расположению ли­ний уровня можно получить представление о форме поверхнос­ти, описываемой функцией Z = F(X, у). Там, где функция изме­няется быстрее, линии уровня сгущаются, а там, где поверх­ность пологая, линии уровня располагаются реже (рис. 8.4).

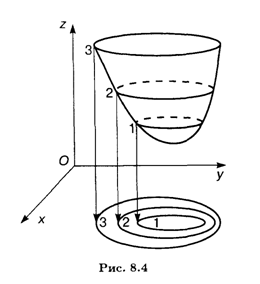
Пример 3. Найти линии уровня функции Z = х2 + у2 — 2Х — 2У.

Решение. Линии уровня данной функции — это семейство кривых на плоскости Оху, описываемое уравнением

Последнее уравнение описывает семейство окружностей с цент­ром в точке O1(l, 1) радиуса R =. Поверхность враще­ния (параболоид), описываемая данной функцией, становится "круче" по мере ее удаления от оси, которая дается уравнени­ями X = 1, У = 1.

< Предыдущая		Следующая >