08.2.2. Понятие функции нескольких переменных

Введем понятие функции нескольких переменных.

Определение 1. Пусть каждой точке М из множества точек {М} евклидова пространства Em по какому-либо закону ста­вится в соответствие некоторое число И из числового множес­тва U. Тогда будем говорить, что на множестве {М} задана функция И = F(M). При этом множества {М} и U называют­ся соответственно областью определения (задания) и областью изменения функции F(M).

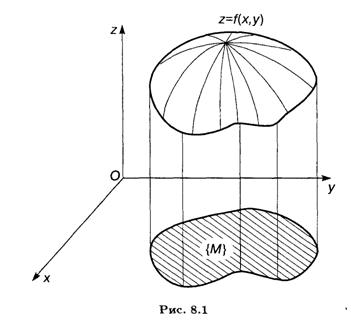
Как известно, функция одной переменной У = F(X) изобра­жается на плоскости в виде линии. В случае двух переменных область определения {Мп} функции Z = F(X, Y) представляет собой некоторое множество точек на координатной плоскости Оху (рис. 8.1). Координата Z называется Аппликатой, и тогда сама функция изображается в виде некоторой поверхности в пространстве E3. Аналогичным образом функция от Т пере­менных

Определенная на множестве {М} евклидова пространства Еm, Представляет собой гиперповерхность в евклидовом простран­стве Еm+1.

< Предыдущая		Следующая >