08.2.1. Множества точек евклидова пространства Еm. Примеры множеств евклидова пространства Еm

Будем обозначать символом {М} некоторое множество то­чек M-мерного пространства Еm. Рассмотрим некоторые при­меры множеств в этом пространстве.

1. Множество {М} всевозможных точек, координаты X1, X2, ..., Xm которых удовлетворяют неравенству

Называется Т-мерным шаром радиуса R с центром в точке M0(x,x,...,x).

Этот пример является M-мерным обобщением соответ­ственно круга на евклидовой плоскости и шара в трехмерном евклидовом пространстве, которые задаются следующими не­равенствами:

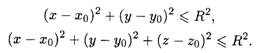
Неравенство (8.2) можно переписать с учетом (8.1) в виде

В случае строгого неравенства ρ(М, М0) < R множество {М} называется Открытым т-мерным шаром. Часто это мно­жество также называют R-окрестностью точки M0. В случае (8.3) если неравенство не строгое, множество {М} называет­ся Замкнутым т-мерным шаром. Эти понятия переносятся на случай любой размерности при Т ≥ 2.

2. Множество {М} точек, таких, что расстояние от каж­дой из них до некоторой точки M0 удовлетворяет равенству ρ(М, М0) = R, называется Т-мерной сферой радиуса R С цент­ром в точке M0.

Аналогия: для плоскости — окружность (X – X0)2 + (у – Y0)2 = R2 радиуса R С центром в точке М0(х0, у0), для пространства — сфера (X – X0)2 + (У – Y0)2 + (Z – Z0)2 = R2 радиуса R С центром в точке М0(х0, у0, z0).

< Предыдущая		Следующая >