07.7. Несобственные интегралы

При рассмотрении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция, во-первых, задана на конечном отрезке и, во-вторых, ограничена. Данное выше определение определенного интегра­ла не имеет смысла при невыполнении хотя бы одного из этих условий. Нельзя разбить бесконечный интервал на конечное число отрезков конечной длины; при неограниченной функции интегральная сумма не имеет предела. Тем не менее возможно обобщить понятие определенного интеграла и на эти случаи, с чем и связано понятие Несобственного интеграла.

Определение. Пусть функция F(X) определена на промежутке [А, +) и интегрируема на любом отрезке [A, R], R > 0, так что интеграл

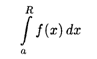
Имеет смысл. Предел этого интеграла при R называется Несобственным интегралом с бесконечным пределом интег­рирования:

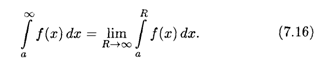
Если этот предел конечен, говорят, что несобственный ин­теграл (7.16) Сходится, а функцию F(X) называют Интегри­руемой на бесконечном промежутке [А, ); если же предел в (7.16) бесконечен или не существует, то говорят, что несобст­венный интеграл Расходится.

Аналогичным образом вводится понятие несобственного интеграла по промежутку (-, B]:

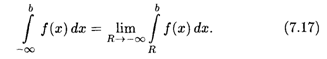
Наконец, несобственный интеграл с двумя бесконечными пре­делами можно определить как сумму несобственных интегра­лов (7.16) и (7.17):

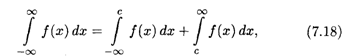
Где С — любое число.

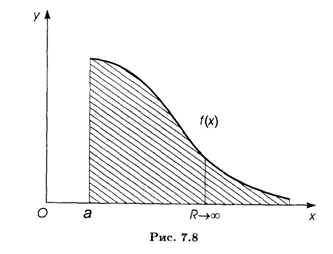
Геометрический смысл несобственного интеграла первого рода заключается в следующем: это площадь бесконечной об­ласти (рис. 7.8), ограниченной сверху неотрицательной функ­цией F(X), снизу — осью Оx, слева — прямой Х = А.

Рассмотрим несколько примеров несобственных интегра­лов.

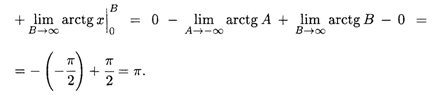
Здесь пришлось разделить исходный интеграл на два и к каж­дому из них применить определение несобственного инте­грала.

Пример 4. , где α — некоторое положительное число.

Решение. Рассмотрим разные случаи для числа α.

1. При α = 1 для любого R > 0 имеем

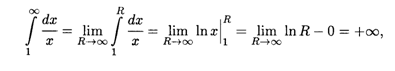
Т. е. конечного предела не существует и несобственный интег­рал расходится.

2. При α ≠ 1 для любого R > 0 получаем

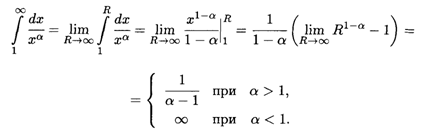
Следовательно, данный интеграл сходится при α > 1 и рас­ходится при α ≤ 1.

В приведенных выше примерах сначала с помощью пер­вообразной вычислялся интеграл по конечному промежутку, а затем осуществлялся переход к пределу. Между тем если для функции F(X) существует первообразная F(X) на всем проме­жутке интегрирования [А,), то по формуле Ньютона-Лейб­ница

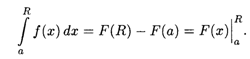
Отсюда следует, что несобственный интеграл существует (схо­дится) в том и только в том случае, когда существует конеч­ный предел

И тогда можно записать:

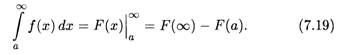
Аналогичный вывод справедлив и для несобственных интегра­лов вида (7.17) и (7.18):

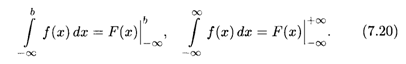
Иными словами, формула Ньютона-Лейбница (основная фор­мула интегрального исчисления) применима и в случае, когда пределы интегрирования бесконечны.

< Предыдущая		Следующая >