07.6.1. Некоторые приложения в экономике. Дневная выработка

Вообще говоря, в экономических задачах переменные меня­ются дискретно. Для использования определенного интеграла нужно составить некоторую идеализированную модель, пред­полагающую непрерывное изменение зависимых переменных (функций) и независимых переменных (аргумента). Рассмот­рим соответствующие примеры.

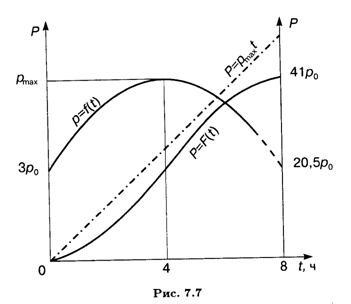
Найти дневную выработку Р за рабочий день продолжи­тельностью восемь часов, если производительность труда в течение дня меняется по эмпирической формуле

Где T — время в часах, Р0 — размерность производительности (объем продукции в час), T0 — размерность времени (ч). Эта формула вполне отражает реальный процесс работы (рис. 7.7): производительность сначала растет, достигая максимума в се­редине рабочего дня при T = 4 ч, а затем падает.

Решение. Полагая, что производительность меняется в те­чение дня непрерывно, т. е. Р является непрерывной функцией аргумента T на отрезке [0, 8], дневную выработку Р можно вы­разить определенным интегралом:

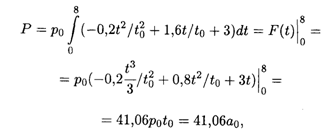
Где А0 — множитель, имеющий размерность единицы продук­ции. Если бы в течение всего дня работа велась ритмично и с максимальной производительностью Ртах = 6,2Р0, то днев­ная выработка составила бы Рmах = 49,6А0, или примерно на 21% больше. Рис. 7.7 иллюстрирует решение задачи: дневная выработка численно равна площади криволинейной трапеции, ограниченной сверху кривой F(T); вторая кривая показывает рост выпуска продукции во времени (график первообразной F(T) соответствует правой оси ординат Р). Значение Т = 4 ч соответствует точке перегиба кривой F(T): в первой половине рабочего дня интенсивность выработки продукции выше, чем во второй. Штрихпунктирная прямая Р = РmахT соответствует выпуску продукции с равномерной производительностью Рmах.

< Предыдущая		Следующая >