07.5.2. Объем тела вращения

Рассмотрим тело, которое образуется при вращении во­круг оси Ох криволинейной трапеции, ограниченной сверху непрерывной и положительной на отрезке [А, b] функцией F(X) (рис. 7.5). Объем этого тела вращения определяется формулой

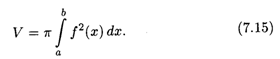
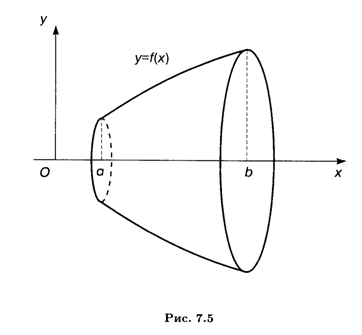
Если тело образовано вращением криволинейной трапеции вокруг оси Оу, то, выражая Х через У как обратную функцию, мы можем получить аналогичным образом формулу для объ­ема тела вращения:

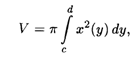
Где [C, D] — область изменения функции У = F(X).

Рассмотрим примеры вычисления объемов тел, образован­ных вращением фигур, ограниченных следующими линиями.

Пример 3. У = х2, у = вокруг оси Ох.

Решение. Искомый объем вращения равен разности объ­емов, образованных вращением криволинейных трапеций с верхними границами соответственно У = и У = Х2. Пределы интегрирования определяются по точкам пересечения этих кривых: А = 0 и B = 1. По формуле (7.15) получаем

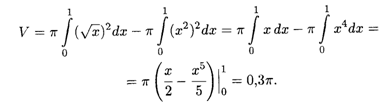
Пример 4. У = eх, х = 0, Х = 1, У = 0 вокруг оси Оу.

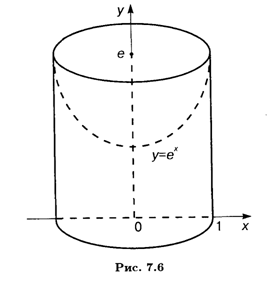
Ррешение. Выражаем Х через У: х = ln У; промежуток ин­тегрирования [1, Е] определяется очевидным образом. Объем тела вращения (рис. 7.6) равен разности объемов соответствен­но цилиндра радиуса 1 и высоты Е и тела вращения вокруг оси Оу криволинейной трапеции, ограниченной сверху кривой Х = ln У. Согласно формуле (7.15) получаем

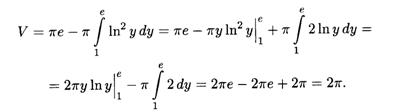
< Предыдущая		Следующая >