07.4.2. Интегрирование по частям в определенном интеграле

ТЕОРЕМА 6. Пусть функции и(х) и V(X) имеют непрерывные производные на отрезке [А, b]; тогда справедлива формула

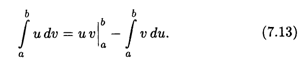
Равенство (7.13) называется Формулой интегрирования по частям в определенном интеграле. Рассмотрим ряд приме­ров вычисления определенных интегралов методом интегриро­вания по частям.

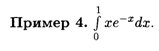
Решение. Положим здесь И = х, V = e-x, тогда Dv = -e-xdx и

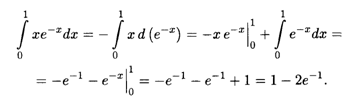
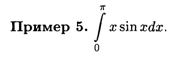
Решение. Здесь И = Х, Sin X Dx = dv или V = - cos X; далее по формуле (7.13) имеем

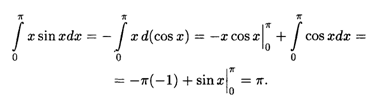
< Предыдущая		Следующая >