07.3. Основная формула интегрального исчисления

ТЕОРЕМА 4. Непрерывная на отрезке [А, b] функция F(X) имеет на этом отрезке первообразную. Одной из первооб­разных является функция

В формуле (7.8) переменная интегрирования обозначена буквой T, чтобы избежать путаницы с верхним переменным пределом Х.

Поскольку всякая другая первообразная отличается от F(X) На постоянную величину, то связь между неопределенным и определенным интегралами имеет вид

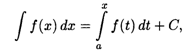
Где С — произвольная постоянная.

Согласно теореме 7.4 непрерывная на отрезке [А, B] функция F(X) имеет первообразную, которая определяется формулой

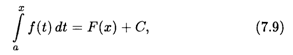
Где С — некоторая постоянная. Подставляя в (7.9) Х = А, с учетом свойства 1 определенного интеграла получаем

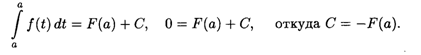
Тогда из (7.9) имеем

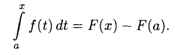
Полагая Х = b, получаем формулу

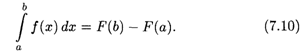
Равенство (7.10) называется Основной формулой интег­рального исчисления, или Формулой Ньютона-Лейбница.

Разность F(B) — F(A) условно записывают символом F(X), т. е.

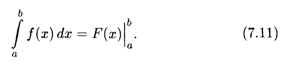
Формула (7.11) дает широкие возможности вычисления оп­ределенных интегралов. Нужно вычислить неопределенный ин­теграл и затем найти разность значений первообразной соглас­но (7.11). Рассмотрим примеры вычисления определенных ин­тегралов.

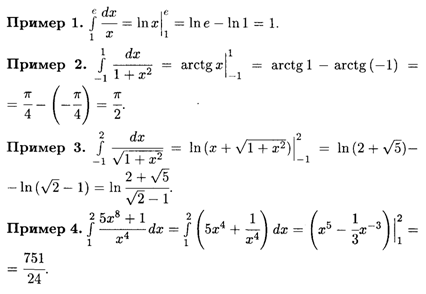
< Предыдущая		Следующая >