07.2. Основные свойства определенного интеграла

1. Интеграл Был определен для случая, когда A < B. Обобщим понятие определенного интеграла и на дру­гие случаи.

По определению полагаем

Как определенный интеграл на отрезке нулевой длины.

Также по определению полагаем, что

Поскольку при движении от B к А все длины частичных отрез­ков ΔXi = Xi-1 — xi имеют отрицательный знак в интегральной сумме (7.1).

2. Для любых чисел а, B и С имеет место равенство

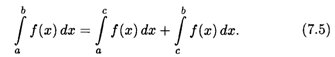
3. Постоянный множитель можно выносить за знак опреде­ленного интеграла:

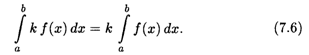
4. Определенный интеграл от алгебраической суммы функ­ций равен алгебраической сумме их определенных интегралов:

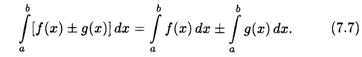
Заметим, что свойство 4 имеет место для любого конечного числа слагаемых.

Будем полагать далее, что А < b.

5. Если функция F(X) ≥ 0 всюду на отрезке [А, b], то

6. Если F(X) ≤ G(х) всюду на отрезке [А, b], то

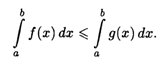
7. Если функция F(X) интегрируема на [А, b], то

8. Если М и Т — соответственно максимум и минимум функции F(X) на отрезке [А, B], то

< Предыдущая		Следующая >