06.4.3. Интегрирование по частям
ТЕОРЕМА 2. Пусть функции и(х) и v(x) определены и дифференцируемы на промежутке Х и функция и'(x)v(x) имеет первообразную на этом промежутке. Тогда функция u(x)v'(x) также имеет первообразную на промежутке X, причем справедлива формула
![]()
С учетом вида дифференциалов функций v'(x)dx = dv и u'(x)dx = du равенство (6.2) часто используют в форме
![]()
Равенство (6.2) (или (6.3)) называется формулой интегрирования по частям.
В интегрировании по частям самым сложным является выбop в подынтегральном выражении сомножителя V'(X) Dx = Dv. Под знак дифференциала D можно в принципе внести все что угодно; однако выбор должен быть таким, чтобы интеграл в правой части (6.2) был проще исходного, а не сложнее. В этом смысле метод интегрирования по частям позволяет свести интеграл ![]() Dv к интегралу
Dv к интегралу ![]() Du, вычислить который существенно проще. Рассмотрим примеры нахождения интегралов методом интегрирования по частям.
Du, вычислить который существенно проще. Рассмотрим примеры нахождения интегралов методом интегрирования по частям.
Пример 8. ![]() DX.
DX.
Решение. Здесь берем И(х) = ln X, Dv = Dx, т. е. V = Х. По формуле (6.2) получаем
![]()
В общем случае интегралы вида ![]() Ln Х dx, где П ≠ 1 — целое число, берутся только интегрированием по частям: И = ln X, Xndx = dv, т. е. V = хn+1 /(П + 1). Аналогичным образом берутся и интегралы вида
Ln Х dx, где П ≠ 1 — целое число, берутся только интегрированием по частям: И = ln X, Xndx = dv, т. е. V = хn+1 /(П + 1). Аналогичным образом берутся и интегралы вида ![]() Arctg X Dx.
Arctg X Dx.
Пример 9. ![]() Dx.
Dx.
Решение. В этом случае И = Х, EХDx = dv = d(ex), тогда по формуле (6.2) имеем
![]()
Интегралы вида ![]() Dx, где П > 0 — целое число и K ≠ 0 — любое число, берутся N-кратным интегрированием по частям до исчезновения степени Х в подынтегральной функции; при этом каждый раз под знак D вносится Еkx, т. е. Ekxdx = Dv =
Dx, где П > 0 — целое число и K ≠ 0 — любое число, берутся N-кратным интегрированием по частям до исчезновения степени Х в подынтегральной функции; при этом каждый раз под знак D вносится Еkx, т. е. Ekxdx = Dv = ![]() D(еkX).
D(еkX).
![]()
Ррешение. Интегралы вида ![]() Cos kx dx и
Cos kx dx и ![]() Sin Kx Dx, где K — любое число и П > 0 — целое число, вычисляются так же, как и интеграл общего вида, приведенный в примере 1. Под знак D каждый раз вносится тригонометрическая функция, и процедура интегрирования по частям повторяется N раз:
Sin Kx Dx, где K — любое число и П > 0 — целое число, вычисляются так же, как и интеграл общего вида, приведенный в примере 1. Под знак D каждый раз вносится тригонометрическая функция, и процедура интегрирования по частям повторяется N раз:
Cos Kx Dx = Dv = ![]() D (sin Kx), затем sin Kx Dx = -
D (sin Kx), затем sin Kx Dx = -![]() D(cos Kx) и т. д.
D(cos Kx) и т. д.
В данном случае мы имеем

Введем понятие Рациональной функции от двух переменных. Это функция, полученная из переменных И и V путем проведения над ними арифметических операций. Например, функция
![]()
Является рациональной от переменных U и V. В свою очередь переменные И и V также могут являться функциями. Например,
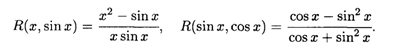
| < Предыдущая | Следующая > |
|---|