06.4.4. Рациональная функция от Sin Х и cos х

Рассмотрим интеграл вида

Где R — рациональная функция. Этот интеграл рационализи­руется универсальной подстановкой

Действительно,

Подстановка формул (6.5) в интеграл (6.4) дает

Где R1(T) — другая рациональная функция аргумента T. Рас­смотрим примеры вычисления интегралов, содержащих рацио­нальные функции от sin X и cos X.

Решение. Подставляя сюда формулы (6.5), после очевид­ных упрощений получаем

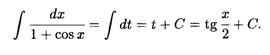
Пример 12. Dx, т И п — натуральные числа.

Решение. Универсальная подстановка приведет здесь к громоздким выкладкам; гораздо удобнее применить метод за­мены переменной. В зависимости от четности M и П употреби­мы три следующих варианта.

1) M — четное, N — нечетное, подстановка T = sin X.

2) Т — нечетное, N — четное; подстановка T = Cos X.

3) M и N — оба нечетные; любая из двух подстановок 1 или 2.

4) M и П — оба четные; понизить степени тригонометри­ческих функций и в полученной сумме проверить каждое сла­гаемое по пп. 1-3.

Например, найти интеграл Dx.

Согласно п. 2 выполним подстановку T = cos X; тогда Dt = - sin X Dx, sin4 X = (1 — T2)2; отсюда имеем

< Предыдущая		Следующая >