05.2.1. Формула Маклорена. Разложение функций по формуле Маклорена
Одним из основных принципов математики является представление сложного через более простое. Формула Маклорена* как раз и является реализацией этого принципа. Любые функции, дифференцируемые достаточное число раз в точке Х = 0, могут быть представлены в виде многочлена некоторой степени. Многочлены же являются наиболее простыми элементарными функциями, над которыми удобно выполнять арифметические действия, вычислять значения в любой точке и т. д.
* Колин Маклорен — шотландский математик (1698 — 1746).
Итак, функцию F(X), имеющую (N + 1) производных в точке Х = 0, можно представить по формуле Маклорена вместе с остаточным членом:
![]()
Формула (5.2) дает возможность разложить функцию F(X) по формуле Маклорена (в окрестности нуля) или, что то же самое, представить F(X) в виде многочлена, коэффициенты которого вычисляются достаточно просто. Эта формула широко используется и для приближенных вычислений значений различных функций; при этом погрешность вычислений оценивается по остаточному члену О(Xn).
Рассмотрим примеры разложения функций по формуле Маклорена.
Пример 1. F(X) = Еx.
Решение. Поскольку (Ex)(N) = Eх, F(n)(0) = Е0 = 1 для любого П, формула Маклорена (5.2) имеет вид
![]()
Формула (5.3) используется для вычисления числа Е с любой необходимой точностью. Отсюда при Х = 1 получаем приближенное значение числа Е ≈ 2,7182818 ....
Пример 2. F(X) = sin X.
Решение. Нетрудно проверить, что F(N)(X) = Sin ![]() ; отсюда имеем
; отсюда имеем
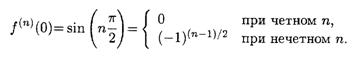
Подстановка в формулу (5.3) приводит к выражению
![]()
Пример 3. F(X) = cos X.
Решение. По аналогии с функцией синуса имеем ![]() , откуда получаем
, откуда получаем
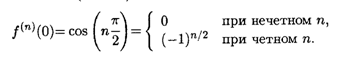
Подстановка в формулу (5.2) приводит к разложению по формуле Маклорена:

Пример 4. F(X) = ln (l + Х).
Решение. Так как ![]() , то F(0) = 0,
, то F(0) = 0, ![]() ; подстановка в формулу (5.2) приводит к разложению функции ln (1 +X) по формуле Маклорена (при этом 0! = 1):
; подстановка в формулу (5.2) приводит к разложению функции ln (1 +X) по формуле Маклорена (при этом 0! = 1):
![]()
Пример 5. F(X) = (1 + X)α, где α — вещественное число.
Решение. Производная N-го порядка имеет вид F(N)(X) = α (α - 1)( α - 2)... (α - N +1)(1 + X) α-N, т. е. F(N)(0) = α (α — 1)... (α - П + 1), и формула Маклорена для данной функции такова:
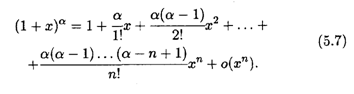
В частном случае, когда α = п — целое число, имеем F(N + l) = 0 и формула (5.7) переходит в формулу Бинома Ньютона:
![]()
Т. е. бином Ньютона является частным случаем формулы Маклорена.
| < Предыдущая | Следующая > |
|---|