05.1.2. Другие виды неопределенностей

Неопределенности вида 0 ∙ и — можно свести к неопределенностям вида и . Покажем это на примерах.

Пример 6. Найти предел X ln X.

Решение. Здесь неопределенность вида 0 ∙ . Преобразуем функцию под знаком предела: Х ln Х = и теперь уже имеем неопределенность вида при Х 0+. Теперь, применяя правило Лопиталя, получаем

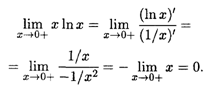
Пример 7. Найти (cosec X — ctg X).

Решение. Это неопределенность вида — . Преобразуя функцию под знаком предела, получаем

Теперь это неопределенность вида при Х 0. Правило Ло­питаля дает нам

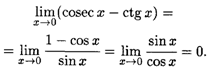
Рассмотрим неопределенности вида 00, 1, 0, возникаю­щие при вычислении пределов функций У = и(х)V(X). Неопреде­ленности этого вида сводятся к неопределенности вида 0 ∙ , уже рассмотренной выше, с помощью тождественного преоб­разования

Пример 8. Найти предел .

Решение. Это предел вида 00; используя формулу (5.1), имеем с учетом решения шестого примера

Пример 9. Найти предел

Решение. Это предел вида 1. Найдем предел функции У = ctg X ln(1 + X) при X 0. В соответствии с представлением (5.1) имеем следующую цепочку равенств:

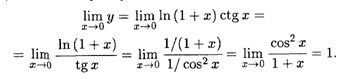
Следовательно, искомый предел равен

< Предыдущая		Следующая >