04.1.1. Геометрический смысл производной
Для выяснения геометрического смысла производной нам понадобится определение касательной к графику функции в данной точке.
Определение 2. Касательной к графику функции У = F(X) в точке М называется предельное положение секущей MN, когда точка N стремится к точке М по кривой F(X).
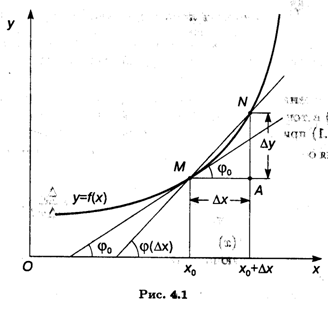
Пусть точка М на кривой F(X) соответствует значению аргумента X0, а точка N — значению аргумента X0 + ΔX (рис. 4.1). Из определения касательной следует, что для ее существования в точке X0 необходимо, чтобы существовал предел ![]() , который равен углу наклона касательной к оси ОX. Из треугольника MNA следует, что
, который равен углу наклона касательной к оси ОX. Из треугольника MNA следует, что
![]()
Если производная функции F(X) в точке X0 существует, то, согласно (4.1), получаем
![]()
Отсюда следует наглядный вывод о том, что Производная F'(X0) Равна угловому коэффициенту (тангенсу угла наклона К положительному направлению оси Ох) касательной к графику функции у = F(X) в Точке М(X0, F(X0)). При этом угол наклона касательной определяется из формулы (4.2):
![]()
| < Предыдущая | Следующая > |
|---|