03.7.2. Непрерывность функции на интервале и отрезке. Классификация точек разрыва функции
Говорят, что функция F(X) непрерывна на интервале (А, B), если она непрерывна в каждой точке этого интервала. Функция F(X) непрерывна на отрезке [А, B], если она непрерывна на интервале (А, B) и непрерывна в точке A справа, а в точке B Слева:
![]()
Точки разрыва, в которых функция не является непрерывной, классифицируются следующим образом.
1. Устранимый разрыв. Точка А называется точкой Устранимого разрыва функции F(X), если предел функции в этой точке существует, но в точке А функция F(X) либо не определена, либо ее значение F(А) не равно пределу в этой точке.
Пример 1. Функция F(X) = ![]() в точке Х = 0, как известно, имеет предел, равный единице (первый замечательный предел). Однако в самой точке Х = 0 эта функция не определена, т. е. здесь разрыв первого вида. Этот разрыв можно устранить (потому он и называется устранимым), если доопределить функцию в этой точке значением предела в ней, т. е. ввести новую функцию
в точке Х = 0, как известно, имеет предел, равный единице (первый замечательный предел). Однако в самой точке Х = 0 эта функция не определена, т. е. здесь разрыв первого вида. Этот разрыв можно устранить (потому он и называется устранимым), если доопределить функцию в этой точке значением предела в ней, т. е. ввести новую функцию

Функция F1(X) является непрерывной на всей числовой прямой.
2. Разрыв первого рода. Точка А называется точкой разрыва Первого рода функции F(X), если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы:
![]() .
.
Пример 2. Рассмотрим функцию
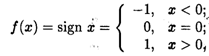
Для нее точка Х = 0 является точкой разрыва 1-го рода.
3. Разрыв второго рода. Точка А называется точкой разрыва Второго рода функции F(X), если в этой точке функция F(X) не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Пример 3. Для функции f(x) = 1/x точка х = 0 является точкой разрыва 2-го рода, поскольку ![]()
![]() .
.
Пример 4. Для функции F(X) = sin (l/X) точка Х = 0 является точкой разрыва 2-го рода, так как ни левого, ни правого предела функции в этой точке не существует.
Пример 5. Рассмотрим функцию F(X) = Е1/X = ехр ![]() (рис. 3.8). Точка Х = 0 является точкой разрыва 2-го рода для этой функции, так как предел слева равен нулю, а предел справа бесконечен:
(рис. 3.8). Точка Х = 0 является точкой разрыва 2-го рода для этой функции, так как предел слева равен нулю, а предел справа бесконечен:
![]()

Рис. 3.8
| < Предыдущая | Следующая > |
|---|