03.2.1. Предел функции. Предел функции в точке
Пусть функция F(X) определена на некотором множестве X. Возьмем из Х последовательность точек
![]()
Сходящуюся к точке А, причем А ![]() Х или A
Х или A ![]() X. Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность
X. Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность
![]()
И правомерно рассмотреть вопрос о ее сходимости.
Определение. Число А называется Пределом функции F(X) в точке А (или пределом функции при Х ![]() А), если для любой cходящейся к А последовательности (3.5) значений аргумента Х, отличных от А, соответствующая последовательность значений функции (3.6) сходится к числу А.
А), если для любой cходящейся к А последовательности (3.5) значений аргумента Х, отличных от А, соответствующая последовательность значений функции (3.6) сходится к числу А.
Для обозначения предельного значения функции используется следующая символика: ![]() F(X)
F(X) ![]() А. Заметим, что функция F(X) может иметь в точке А только одно предельное значение, поскольку последовательность F(Xn) имеет только один предел.
А. Заметим, что функция F(X) может иметь в точке А только одно предельное значение, поскольку последовательность F(Xn) имеет только один предел.
Приведем несколько примеров.
Пример 1. Функция F(X) = С = const имеет предел в каждой точке числовой прямой. Действительно, любой последовательности (3.5), сходящейся к точке А, соответствует последовательность (3.6), состоящая из одного и того же числа C, откуда следует, что F(Xn) ![]() С при N
С при N ![]() .
.
Пример 2. Функция F(X) = Х в любой точке А числовой прямой имеет предел, равный А. Действительно, последовательности значений аргумента (3.5) и значений функции (3.6) в этом случае тождественны, и если последовательность {Xn} сходится к А, то и последовательность {F(Xn)} также сходится к А.
Пример 3. Функция F(X) = ![]() имеет в точке X = 0 предел, равный -2. Действительно, пусть {Xn} — любая последовательность значений аргумента, сходящаяся к нулю, т. е. lim Xп = 0 при N
имеет в точке X = 0 предел, равный -2. Действительно, пусть {Xn} — любая последовательность значений аргумента, сходящаяся к нулю, т. е. lim Xп = 0 при N ![]() , тогда в силу свойств последовательностей 1—9 имеем
, тогда в силу свойств последовательностей 1—9 имеем
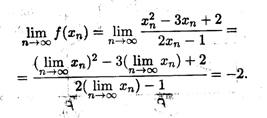
| < Предыдущая | Следующая > |
|---|