03.1.2. Область определения функции

Остановимся на процедуре нахождения области определе­ния функции.

1. В том случае, когда функция задана в аналитическом виде (посредством формулы)

(3.1)

И никаких ограничений или оговорок более не имеется, область ее определения устанавливается исходя из правил выполнения математических операций, входящих в формулу F в (3.1). Эти ограничения хорошо известны: подкоренное выражение в кор­не четной степени не может быть отрицательным, знаменатель дроби не может быть равным нулю, выражение под знаком ло­гарифма должно быть только

Положительным, а также неко­торые другие. Приведем здесь два примера.

Пример 1. У = log2 (X2 — 5X + 6).

Область определения этой функции находится из условия X2 — 5X + 6 > 0. Поскольку X = 2 и X = 3 — корни квадратно­го трехчлена, стоящего под знаком логарифма, то это условие выполняется на двух полубесконечных интервалах: (-, 2) и (3, ). На рис. 3.4 выделена заштрихованная полоса, в которой график функции отсутствует.

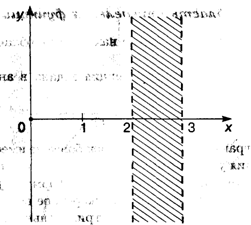
Рис. 3.4

Пример 2. У = arcsin .

Область определения этой функции находится из совокуп­ности двух условий: аргумент под знаком arcsin не может быть по модулю больше единицы и знаменатель аргумента не дол­жен равняться нулю, т. е.

Двойное неравенство эквивалентно двум более простым нера­венствам: Х + 2 ≥ 1 и Х + 2 ≤ -1. Отсюда получаем, что область определения функции состоит из двух полубесконечных проме­жутков: (-, -3] и (-1, ). Запретная точка Х = -2 сюда не попадает. В отличие от предыдущего примера концы полуин­тервалов входят в область определения функции.

2. Область определения функции задана вместе с функцией F(X).

Пример 3. У = 3X-4­­/3 + 2, 1 ≤ Х ≤ 4.

3. Функция имеет определенный прикладной характер, и область ее существования определяется также и реальными значениями входящих параметров (например, задачи с физи­ческим смыслом).

Определение 2. Функция У = F(X) называется Четной (сим­метрия относительно оси Оу), если для любых значений аргу­мента из области ее определения выполнено равенство

Определение 3. Функция У = F(X) называется Нечетной (симметрия относительно начала координат О), если выпол­нено условие:

Например, функции У = х2 и У = cos X являются четными, а функции У = X3 и У = sin X— нечетными.

< Предыдущая		Следующая >