03.1.1. Способы задания функций

Задать функцию — значит указать закон, по которому, со­гласно определению, каждому значению аргумента из области определения ставится в соответствие (вычисляется) значение зависимой переменной из области значений функции. Сущест­вуют три основных способа задания функций: Табличный, ана­литический и графический.

1. Табличный способ. Этот способ имеет широкое при­менение в разных отраслях знаний и приложениях: ряды экспе­риментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т. п. Как правило, в таких таблицах по крайней мере одну из пе­ременных можно принять за независимую (например, время), тогда другие величины будут являться функциями от этого аргумента. По сути дела базы данных основаны на табличном способе задания, хранения и обработки информации, а значит, и на табличной форме функциональной зависимости.

2. Аналитический способ. Этот способ состоит в зада­нии связи между аргументом и функцией в виде формул. Сле­дует подчеркнуть, что функция может определяться и набором формул — на разных промежутках области определения функции используются разные формулы.

Приведем примеры аналитического задания функций.

Пример 1. У = Х3. Эта функция задана на бесконечной пря­мой - < X < . Множество значений этой функции тоже бесконечная числовая прямая - < У < . Функция называ­ется кубической параболой (рис. 3.1).

Рис. 3.1

Пример 2. У = . Функция задана на отрезке [—1, 1], множество ее значений — отрезок [0, 1]. Это половина окруж­ности, лежащая в верхней полуплоскости (рис. 3.2).

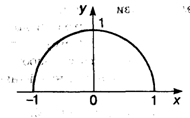
Рис. 3.2

+1, если X > 0;

Пример 3. У = sign X = 0, если Х = 0;

-1, если Х < 0.

Термин sign происходит от латинского signum — Знак. Функ­ция задана на всем бесконечном промежутке (-,), а область ее значений состоит из трех чисел: —1, 0, 1 (рис. 3.3).

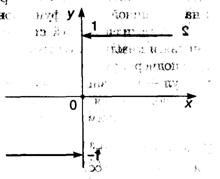
Рис. 3.3

Стрелки означают, что полупрямые не достигают точек ни оси ординат, так как при Х = 0 значение функции определено по другому соответствию.

3. Графический способ. Здесь соответствие между аргу­ментом и функцией задается посредством графика. Этот спо­соб обычно используется в экспериментальных измерениях с употреблением самопишущих приборов (осциллографы, сейс­мографы и т. п.).

< Предыдущая		Следующая >