02.1. Предел последовательности. Числовые последовательности
Числовые последовательности представляют собой бесконечные множества чисел. Примерами последовательностей могут служить: последовательность всех членов бесконечной геометрической прогрессии, последовательность приближенных значений ![]() (X1 = 1, Х2 = 1,4, Х3 = 1,41, ...), последовательность периметров правильных N-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности.
(X1 = 1, Х2 = 1,4, Х3 = 1,41, ...), последовательность периметров правильных N-угольников, вписанных в данную окружность. Уточним понятие числовой последовательности.
Определение 1. Если каждому числу N из натурального ряда чисел 1, 2, 3,..., П,... поставлено в соответствие вещественное число Xп, то множество вещественных чисел
X1, x2, x3, …, xn, … (2.1)
Называется Числовой последовательностью, или просто последовательностью. .
Числа Х1, X2, X3, ..., Xп, ... будем называть Элементами, или Членами последовательности (2.1), символ Xп — Общим элементом, или членом последовательности, а число П — Его Номером. Сокращенно последовательность (2.1) будем обозначать символом {хп}. Например, символ {1/N} обозначает последовательность чисел
![]() .
.
Иными словами, под последовательностью можно понимать бесконечное множество занумерованных элементов или множество пар чисел (п, xп), в которых первое число принимает последовательные значения 1, 2, 3, ... . Последовательность считается заданной, если указан способ получения любого ее элемента. Например, формула XП = -1 + (-1)N определяет последовательность 0, 2, 0, 2,... .
Геометрически последовательность изображается на числовой оси в виде последовательности точек, координаты которых равны соответствующим членам последовательности. На рис. 2.1 изображена последовательность {Хп} = {1/N} на числовой прямой.
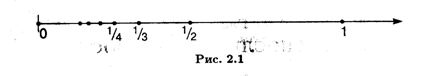
| < Предыдущая | Следующая > |
|---|