02.1.1. Понятие сходящейся последовательности

Определение 2. Число А называется Пределом последова­тельности {Xn}, если для любого положительного числа ε су­ществует такой номер N, что при всех П > N выполняется неравенство

(2.2)

Последовательность, имеющая предел, называется Сходя­щейся. Если последовательность имеет своим пределом число А, то это записывается так:

Последовательность, не имеющая предела, называется Рас­ходящейся.

Определение 3. Последовательность, имеющая своим преде­лом число А = 0, называется Бесконечно малой последователь­ностью.

Замечание 1. Пусть последовательность {Хп} имеет своим пределом число А. Тогда последовательность {αN}= {Xn — a} есть бесконечно малая, т. е. любой элемент Xп Сходящейся последовательности, имеющей предел А, можно представить в виде

Где αN — Элемент бесконечно малой последовательности {αN}.

Замечание 2. Неравенство (2.2) эквивалентно неравен­ствам (см. свойство 4 модуля числа из п. 1.5)

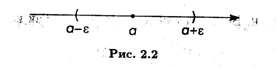
Это означает, что при П > N все элементы последователь­ности {Xn} находятся в ε-окрестности точки А (рис. 2.2), причем номер N определяется по величине ε.

Интересно дать геометрическую интерпретацию этого определения. Поскольку последовательность представляет со­бой бесконечное множество чисел, то если она сходится, в лю­бой ε-окрестности точки А на числовой прямой находится бес­конечное число точек — элементов этой последовательности, тогда как вне ε-окрестности остается конечное число элемен­тов. Поэтому предел последовательности часто называют Точ­кой сгущения.

Замечание 3. Неограниченная последовательность не имеет Конечного предела. Однако она может иметь Бесконеч­ный предел, что записывается в следующем виде:

(2.3)

Если при этом начиная с некоторого номера все члены по­следовательности положительны (отрицательны), то пишут

Если {Xn} — бесконечно малая последовательность, то {1/xп} — Бесконечно большая последовательность, имеющая бесконечный предел в смысле (2.3), и наоборот.

Приведем примеры сходящихся и расходящихся последова­тельностей.

Пример 1. Показать, используя определение предела последовательности, что .

Решение. Возьмем любое число ε > 0. Так как

То чтобы выполнялось неравенство (2.2), достаточно решить неравенство 1 / (N + 1) < ε, откуда получаем N > (1 — ε) / ε. Доста­точно принять N = [(1 — ε)/ε] (целая часть числа (1 — ε)/ ε)* , чтобы неравенство |xп — 1| < ε выполнялось при всех П > N.

* Символ [A] означает целую часть числа А, т. е. наибольшее целое число, не превосходящее А. Например, [2] = 2, [2,5] = 2, [0,8] = 0, [-0, 5] = -1, [-23,7] = -24.

Пример 2. Показать, что последовательность {Хп} = (-1)N, или -1, 1, -1, 1,... не имеет предела.

Решение. Действительно, какое бы число мы ни предпо­ложили в качестве предела: 1 или —1, при ε < 0,5 неравенство (2.2), определяющее предел последовательности, не удовлетво­ряется — вне ε - окрестности этих чисел остается бесконечное число элементов XП: все элементы с нечетными номерами рав­ны —1, элементы с четными номерами равны 1.

< Предыдущая		Следующая >