02.1.2. Основные свойства сходящихся последовательностей
Приведем основные свойства сходящихся последовательностей, которые в курсе высшей математики сформулированы в виде теорем.
1. Если все элементы бесконечно малой последовательности {Хп} равны одному и тому же числу с, то с = 0.
2. Сходящаяся последовательность имеет только один предел.
3. Сходящаяся последовательность ограничена.
4. Сумма (разность) сходящихся последовательностей {Хп} и {Уп} есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей {Xп} и {YП}.
5. Произведение сходящихся последовательностей {Хп} и {Уп} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {Хп} и {Уп}.
6. Частное двух сходящихся последовательностей {Хп} и {Уп} при условии, что предел последовательности {Уп} отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {Хп} и {YП}.
7. Если элементы сходящейся последовательности {Хn} удовлетворяют неравенству xп ≥ b (хп ≤ b) начиная с некоторого номера, то и предел а этой последовательности удовлетворяет неравенству а ≥ B (а ≤ b).
8. Произведение бесконечно малой последовательности на ограниченную последовательность или на число есть бесконечно малая последовательность.
9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Рассмотрим применение этих свойств на примерах.
Пример 3. Найти предел ![]() .
.
Решение. При N ![]() числитель и знаменатель дроби стремятся к бесконечности, т. е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на N2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим
числитель и знаменатель дроби стремятся к бесконечности, т. е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на N2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим

![]()
Пример 4. Найти предел последовательности {Xп} = ![]() при П
при П ![]() .
.
Решение. Здесь, как и в предыдущем примере, числитель и знаменатель не имеют конечных пределов, и потому сначала необходимо выполнить соответствующие преобразования. Поделив числитель и знаменатель на N, получаем
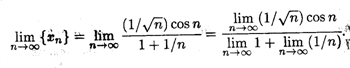
Поскольку в числителе стоит произведение бесконечно малой последовательности на ограниченную последовательность, то в силу свойства 8 окончательно получаем
![]()
Пример 5. Найти предел последовательности {Хп} = ![]() при П
при П ![]() .
.
Решение. Здесь применить непосредственно теорему о пределе суммы (разности) последовательностей нельзя, так как не существует конечных пределов слагаемых в формуле для {Хп}. Умножим и разделим формулу для {ХN} на сопряженное выражение ![]() :
:

Число е
Рассмотрим последовательность {Хп}, общий член которой выражается формулой
![]()
В курсе математического анализа доказывается, что эта последовательность Монотонно возрастает и имеет предел. Этот предел называют числом Е. Следовательно, по определению
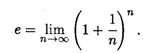
Число Е играет большую роль в математике. Далее будет рассмотрен способ его вычисления с любой требуемой точностью. Отметим здесь, что число Е является иррациональным; его приближенное значение равно Е = 2,7182818... .
| < Предыдущая | Следующая > |
|---|